题目内容
一条直线若同时平行于两个相交平面,则这条直线与这两个平面的交线的位置关系是( )
| A.异面 | B.平行 | C.相交 | D.不确定 |
B
如图所示,直线a∥α,a∥β,α∩β=b,求证a∥b.只需考虑线面平行的性质定理及平行公理即可.
解:由a∥α得,经过a的平面与α相交于直线c,
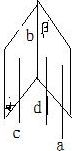
则a∥c,
同理,设经过a的平面与β相交于直线d,
则a∥d,由平行公理得:c∥d,
则c∥β,又c?α,α∩β=b,所以c∥b,
又a∥c,所以a∥b.
故答案为B.
解:由a∥α得,经过a的平面与α相交于直线c,

则a∥c,
同理,设经过a的平面与β相交于直线d,
则a∥d,由平行公理得:c∥d,
则c∥β,又c?α,α∩β=b,所以c∥b,
又a∥c,所以a∥b.
故答案为B.

练习册系列答案
相关题目
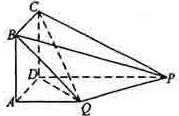
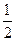 PD.
PD.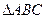 中,
中,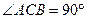 ,
,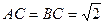 ,
,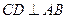 ,
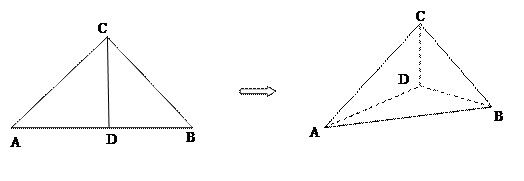
,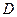 为垂足.沿
为垂足.沿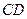 将
将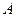 、
、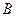 ,使得
,使得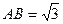 .
.
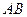 上是否存在点
上是否存在点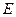 ,使
,使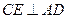 ?若存在,求出
?若存在,求出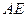 的长;若不存在,说明理由;
的长;若不存在,说明理由; 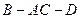 的平面角的大小.
的平面角的大小.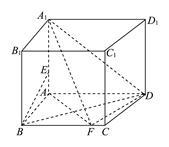
 边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
边形ABCD是边长为2的正方形,AE=EB,F为CE上的点,且BF⊥平面ACE.
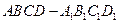 中,
中,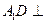 平面
平面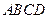 ,底面
,底面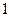 的正方形,侧棱
的正方形,侧棱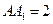 .
.
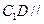 平面
平面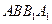 ;
;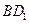 与平面
与平面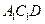 所成角的正弦值.
所成角的正弦值.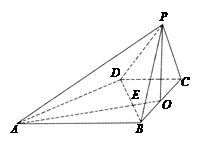
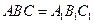 中,AB⊥BC,D为AC的中点,
中,AB⊥BC,D为AC的中点,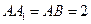 。
。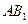 ∥平面
∥平面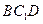 ;
;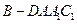 的体积为2,求二面角
的体积为2,求二面角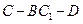 的正切值。
的正切值。
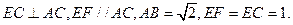

 平
平 面DEF;
面DEF; 角A—BF—E的大小。
角A—BF—E的大小。