题目内容
已知正方形ABCD的边长为4，对角线AC与BD交于点O，将正方形ABCD沿对角线BD折成60°的二面角，A点变为A′点．给出下列判断：①A′C⊥BD；②A′D⊥CO；③△A′OC为正三角形；④cos∠A′DC=
；⑤A′到平面BCD的距离为
．其中正确判断的个数为（ ）
| 3 |
| 4 |
| 6 |
分析：折起后A到A′，知∠A′OC即为二面角A′-BD-C的平面角，即∠A′OC=60°，且A′O=OC．△A′OC为正三角形；由BD⊥平面A′OC，知BD⊥A′C；在△A′DC中，A′D=DC=4，
A′C=A′O=2
，由余弦定理知cos∠A′DC=
；正△A′OC的边OC上的高为A′到平面BCD的距离为
．
A′C=A′O=2
| 2 |
| 3 |
| 4 |
| 6 |
解答：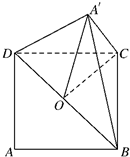
解：如图所示，正方形ABCD沿对角线BD折成60°的二面角后，A点变为A′点，
∴∠A′OC即为二面角A′-BD-C的平面角，即∠A′OC=60°，
∵A′O=OC，∴△A′OC为正三角形，故③正确；
∵BD⊥平面A′OC，故BD⊥A′C，即①正确；
在△A′DC中，A′D=DC=4，A′C=A′O=2
，
由余弦定理知cos∠A′DC=
，故④正确；
正△A′OC的边OC上的高为A′到平面BCD的距离为
．⑤正确，而②不正确；
∴正确的判断有4个．
答案：C
解：如图所示，正方形ABCD沿对角线BD折成60°的二面角后，A点变为A′点，∴∠A′OC即为二面角A′-BD-C的平面角，即∠A′OC=60°，
∵A′O=OC，∴△A′OC为正三角形，故③正确；
∵BD⊥平面A′OC，故BD⊥A′C，即①正确；
在△A′DC中，A′D=DC=4，A′C=A′O=2
| 2 |
由余弦定理知cos∠A′DC=
| 3 |
| 4 |
正△A′OC的边OC上的高为A′到平面BCD的距离为
| 6 |
∴正确的判断有4个．
答案：C
点评：本题考查空间点、线、面的间的距离计算，综合性强，难度大，是高考的重点．解题时要认真审题，仔细解答，注意合理地进行等价转化．
练习册系列答案
相关题目
已知正方形ABCD的边长为2，中心为O，四边形PACE是直角梯形，设PA⊥平面ABCD，且PA=2，CE=1，
如图，已知正方形ABCD的中心为E（-1，0），一边AB所在的直线方程为x+3y-5=0，求其它三边所在的直线方程．已知正方形ABCD的边长为1，设
=
，
=
，
=
，则|
-
+
|等于（ ）
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|