题目内容
 如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.
如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.分析:先求正方形中心E(-1,0)到直线x+3y-5=0的距离,然后设出所求直线方程,利用正方形的中心到三边等距离,分别求出所求直线的方程.
解答:解:E到直线x+3y-5=0距离是
=
,所以E到另三边距离也是
有一条边CD与AB:x+3y-5=0平行,设为x+3y+a=0,则
=
,即|a-1|=6
∴a=-5,a=7 其中a=-5就是已知的
∴CD方程为:x+3y+7=0
另两条和他们垂直,所以斜率为3,设为:3x-y+b=0
则
=
,即|b-3|=6
∴b=9,b=-3
∴AD的方程:3x-y-3=0;BC的方程:3x-y+9=0
| |-1+0-5| | ||
|
3
| ||
| 5 |
3
| ||
| 5 |
有一条边CD与AB:x+3y-5=0平行,设为x+3y+a=0,则
| |-1+0+a| | ||
|
3
| ||
| 5 |
∴a=-5,a=7 其中a=-5就是已知的
∴CD方程为:x+3y+7=0
另两条和他们垂直,所以斜率为3,设为:3x-y+b=0
则
| |-3+0+b| | ||
|
3
| ||
| 5 |
∴b=9,b=-3
∴AD的方程:3x-y-3=0;BC的方程:3x-y+9=0
点评:本题考查点到直线的距离公式,直线的平行和垂直关系,利用正方形的中心到三边等距离是解题的关键,是基础题.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
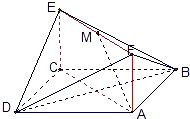 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,AB= 如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当
如图,已知正方形ABCD的边长为1,过正方形中心O的直线MN分别交正方形的边AB,CD于M,N,则当 如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF=
如图,已知正方形ABCD和梯形ACEF所在平面互相垂直,AB=2,AF= 如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直,
如图,已知正方形ABCD和矩形ACEF所在的平面互相垂直, (2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.
(2012•深圳二模)如图,已知正方形ABCD在水平面上的正投影(投影线垂直于投影面)是四边形A′B′C′D′,其中A与A'重合,且BB′<DD′<CC′.