题目内容
已知正方形ABCD的边长为1，设
=
，
=
，
=
，则|
-
+
|等于（ ）
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|
分析：由题意得
+
=
，|
|=
，故有|
-
+
|=|2
|，由此求出结果．
| a |
| b |
| c |
| c |
| 2 |
| a |
| b |
| c |
| a |
解答：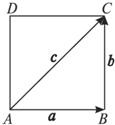
解析：如图，
+
=
，
故
+
+
= 2
．
有|
-
+
|=|2
|，
又|
|=1
∴有|
-
+
|=2，
故选C．
解析：如图，| a |
| b |
| c |
故
| a |
| b |
| c |
| c |
有|
| a |
| b |
| c |
| a |
又|
| a |
∴有|
| a |
| b |
| c |
故选C．
点评：本题考查两个向量的加减法的法则，以及其几何意义，向量的模的定义，求向量的模的方法，运用向量和的三角形法则求出向量的和是解题的关键．
练习册系列答案
相关题目
已知正方形ABCD的边长为2，中心为O，四边形PACE是直角梯形，设PA⊥平面ABCD，且PA=2，CE=1，
如图，已知正方形ABCD的中心为E（-1，0），一边AB所在的直线方程为x+3y-5=0，求其它三边所在的直线方程．