题目内容
 已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1,
已知正方形ABCD的边长为2,中心为O,四边形PACE是直角梯形,设PA⊥平面ABCD,且PA=2,CE=1,(1)求证:面PAD∥面BCE.
(2)求PO与平面PAD所成角的正弦.
(3)求二面角P-EB-C的正切值.
分析:(1)通过线线平行⇒线面平行⇒面面平行;
(2)根据面面垂直的性质作交线的垂线,再证线面垂直,证射影,证明角符合定义,然后求角即可;
(3)根据线面垂直关系利用三垂线定理,作二面角的平面角,通过解三角形求解.
(2)根据面面垂直的性质作交线的垂线,再证线面垂直,证射影,证明角符合定义,然后求角即可;
(3)根据线面垂直关系利用三垂线定理,作二面角的平面角,通过解三角形求解.
解答:解:(1)证明:
∵PA∥CE,AD∥BC,PA∩AD=A,
BC,CE?平面BCE,∴平面PAD∥平面BCE.
(2)∵PA⊥平面ABCD,PA?平面PAD,∴平面PAD⊥平面ABCD,
过O作OG⊥AD于G,连接PG.
∵OG⊥平面PAD,∴PG是PO在平面PAD内的射影,
∴∠POG为PO与平面PAD所成的角.
在Rt△PAO中,OP=
=
在△PGO中,∠PGO=
,OG=1,
∴sin∠POG=
=
.
∴PO与平面PAD所成角的正弦为
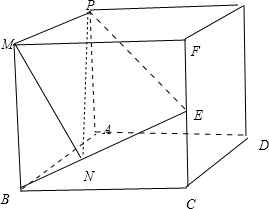
(3)把图形补成如图正方体形状,过M作MN⊥BE于N,连接PN.
∵PM⊥平面BCFM,∴MN为PN在平面BCFM中的射影,
由三垂线定理得PN⊥BE,∴∠PNM为二面角P-BE-C的平面角的补角,
∵tan∠BEC=tan∠MBN=2,∴sin∠MBN=
,
MN=2×sin∠MBN=
在Rt△PMN中,tan∠MNB=
=
.
所求二面角的正切值为-

∵PA∥CE,AD∥BC,PA∩AD=A,
BC,CE?平面BCE,∴平面PAD∥平面BCE.
(2)∵PA⊥平面ABCD,PA?平面PAD,∴平面PAD⊥平面ABCD,
过O作OG⊥AD于G,连接PG.
∵OG⊥平面PAD,∴PG是PO在平面PAD内的射影,
∴∠POG为PO与平面PAD所成的角.
在Rt△PAO中,OP=
| PA2+OA2 |
| 6 |
在△PGO中,∠PGO=
| π |
| 2 |
∴sin∠POG=
| 1 | ||
|
| ||
| 6 |
∴PO与平面PAD所成角的正弦为
| ||
| 6 |

(3)把图形补成如图正方体形状,过M作MN⊥BE于N,连接PN.
∵PM⊥平面BCFM,∴MN为PN在平面BCFM中的射影,
由三垂线定理得PN⊥BE,∴∠PNM为二面角P-BE-C的平面角的补角,
∵tan∠BEC=tan∠MBN=2,∴sin∠MBN=
| 2 | ||
|
MN=2×sin∠MBN=
4
| ||
| 5 |
在Rt△PMN中,tan∠MNB=
| PM |
| MN |
| ||
| 2 |
所求二面角的正切值为-
| ||
| 2 |
点评:本题考查面面平行的判定及空间角的求法.求空间角的一般步骤是:1、作角(根据定义作平行线或垂线);2、证角(证明符合定义);3、求角(解三角形).空间中直线与平面所成的角的范围是:[0,
];二面角的取值范围是:[0,π].
| π |
| 2 |

练习册系列答案
相关题目
已知正方形ABCD的边长为1,设
=
,
=
,
=
,则|
-
+
|等于( )
| AB |
| a |
| BC |
| b |
| AC |
| c |
| a |
| b |
| c |
| A、0 | ||
B、
| ||
| C、2 | ||
D、2
|
 如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.
如图,已知正方形ABCD的中心为E(-1,0),一边AB所在的直线方程为x+3y-5=0,求其它三边所在的直线方程.