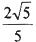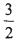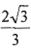题目内容
已知椭圆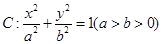 的离心率为
的离心率为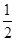 ,直线
,直线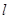 过点
过点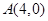 ,
,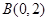 ,且与椭圆
,且与椭圆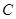 相切于点
相切于点 .
.
(Ⅰ)求椭圆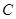 的方程;
的方程;
(Ⅱ)过点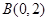 的动直线与曲线
的动直线与曲线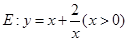 相交于不同的两点
相交于不同的两点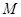 、
、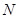 ,曲线
,曲线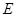 在点
在点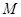 、
、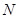 处的切线交于点
处的切线交于点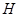 .试问:点
.试问:点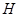 是否在某一定直线上,若是,试求出定直线的方程;否则,请说明理由.
是否在某一定直线上,若是,试求出定直线的方程;否则,请说明理由.
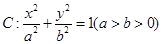 的离心率为
的离心率为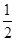 ,直线
,直线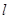 过点
过点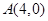 ,
,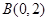 ,且与椭圆
,且与椭圆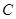 相切于点
相切于点 .
. (Ⅰ)求椭圆
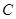 的方程;
的方程;(Ⅱ)过点
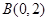 的动直线与曲线
的动直线与曲线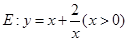 相交于不同的两点
相交于不同的两点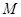 、
、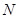 ,曲线
,曲线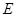 在点
在点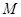 、
、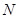 处的切线交于点
处的切线交于点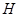 .试问:点
.试问:点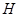 是否在某一定直线上,若是,试求出定直线的方程;否则,请说明理由.
是否在某一定直线上,若是,试求出定直线的方程;否则,请说明理由.解: (Ⅰ)由题得过两点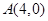 ,
,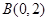 直线
直线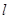 的方程为
的方程为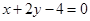 .………… 1分
.………… 1分
因为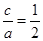 ,所以
,所以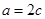 ,
,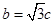 . 设椭圆方程为
. 设椭圆方程为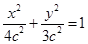 ,
,
由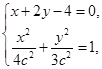 消去
消去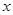 得,
得,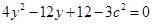 .
.
又因为直线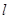 与椭圆
与椭圆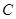 相切,所以
相切,所以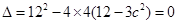 ,解得
,解得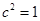 .
.
所以椭圆方程为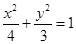 .……………………………………………… 4分
.……………………………………………… 4分
(Ⅱ)易知直线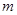 的斜率存在,设直线
的斜率存在,设直线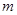 的方程为
的方程为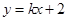 ,…………………… 5分
,…………………… 5分
由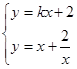 ,消去
,消去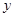 ,整理得
,整理得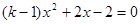 . ………… 6分
. ………… 6分
设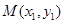 ,
,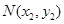 , 由题意知
, 由题意知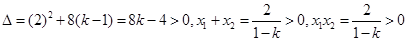 , 解得
, 解得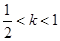 .…8分
.…8分
由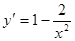 知过点
知过点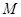 的切线方程为
的切线方程为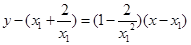
过点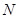 的切线方程为
的切线方程为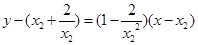 ……………… 10分
……………… 10分
两直线的交点坐标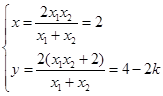 ,
,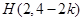
所以点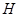 所在的直线方程为
所在的直线方程为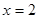 . ………………………………… 13分
. ………………………………… 13分
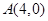 ,
,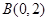 直线
直线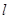 的方程为
的方程为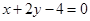 .………… 1分
.………… 1分因为
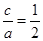 ,所以
,所以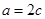 ,
,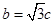 . 设椭圆方程为
. 设椭圆方程为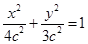 ,
,由
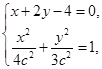 消去
消去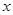 得,
得,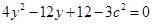 .
.又因为直线
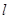 与椭圆
与椭圆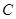 相切,所以
相切,所以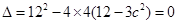 ,解得
,解得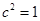 .
.所以椭圆方程为
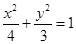 .……………………………………………… 4分
.……………………………………………… 4分(Ⅱ)易知直线
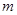 的斜率存在,设直线
的斜率存在,设直线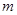 的方程为
的方程为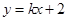 ,…………………… 5分
,…………………… 5分由
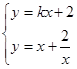 ,消去
,消去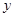 ,整理得
,整理得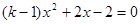 . ………… 6分
. ………… 6分设
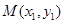 ,
,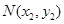 , 由题意知
, 由题意知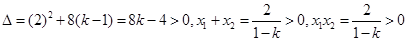 , 解得
, 解得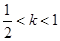 .…8分
.…8分由
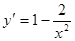 知过点
知过点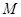 的切线方程为
的切线方程为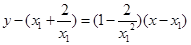
过点
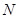 的切线方程为
的切线方程为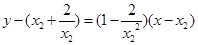 ……………… 10分
……………… 10分两直线的交点坐标
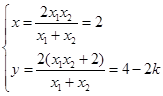 ,
,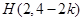
所以点
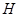 所在的直线方程为
所在的直线方程为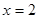 . ………………………………… 13分
. ………………………………… 13分略

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
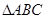 是等腰三角形,
是等腰三角形,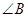 =
=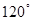 ,则以
,则以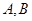 为焦点且过点
为焦点且过点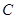 的双曲线的离心率为
的双曲线的离心率为 



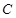 :
: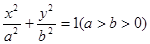 . 称圆心在原点
. 称圆心在原点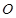 ,半径为
,半径为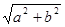 的圆是椭圆
的圆是椭圆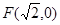 ,其短轴上的一个端点到
,其短轴上的一个端点到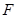 的距离为
的距离为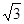 .
.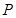 是椭圆
是椭圆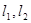 ,使得
,使得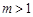 ,直线
,直线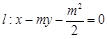 ,椭圆
,椭圆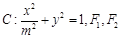 分别为椭圆
分别为椭圆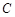 的左、右焦点.
的左、右焦点.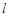 过右焦点
过右焦点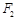 时,求直线
时,求直线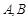 两点,
两点,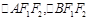 的重心分别为
的重心分别为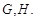 若原点
若原点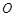 在以线段
在以线段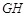 为直径的圆内,求实数
为直径的圆内,求实数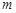 的取值范围.
的取值范围.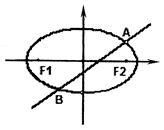
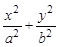 =1(a>b>0)的一个顶点和一个焦点,则此椭圆的离心率e=
=1(a>b>0)的一个顶点和一个焦点,则此椭圆的离心率e=

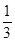
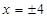 ,离心率为
,离心率为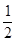 的椭圆方程是( )
的椭圆方程是( )

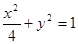
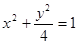
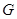 的中心在坐标原点,其中一个焦点为圆
的中心在坐标原点,其中一个焦点为圆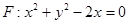 的圆心,右顶点是圆F与x轴的一个交点.已知椭圆
的圆心,右顶点是圆F与x轴的一个交点.已知椭圆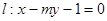 相交于A、B两点.
相交于A、B两点.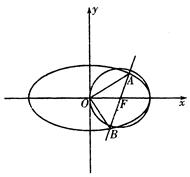
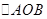 面积的最大值;
面积的最大值;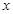 轴上的椭圆
轴上的椭圆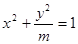 的离心率为
的离心率为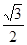 ,则
,则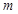 的值是___________。
的值是___________。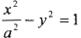 的一个焦点为(2,0),则它的离心率为( )
的一个焦点为(2,0),则它的离心率为( )