题目内容
已知圆(x-2)2+y2=1经过椭圆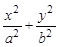 =1(a>b>0)的一个顶点和一个焦点,则此椭圆的离心率e=
=1(a>b>0)的一个顶点和一个焦点,则此椭圆的离心率e=
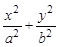 =1(a>b>0)的一个顶点和一个焦点,则此椭圆的离心率e=
=1(a>b>0)的一个顶点和一个焦点,则此椭圆的离心率e=| A.1 | B. | C. | D.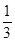 |
D
有图形位置关系知:园过点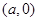 和点
和点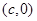 C为半焦距,于是
C为半焦距,于是
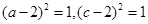 由于
由于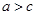 解得
解得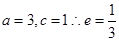 故选D
故选D
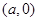 和点
和点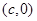 C为半焦距,于是
C为半焦距,于是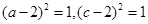 由于
由于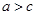 解得
解得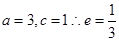 故选D
故选D
练习册系列答案
相关题目
题目内容
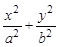 =1(a>b>0)的一个顶点和一个焦点,则此椭圆的离心率e=
=1(a>b>0)的一个顶点和一个焦点,则此椭圆的离心率e=| A.1 | B. | C. | D.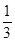 |
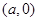 和点
和点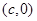 C为半焦距,于是
C为半焦距,于是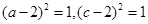 由于
由于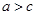 解得
解得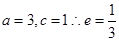 故选D
故选D