题目内容
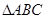 是等腰三角形,
是等腰三角形,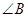 =
=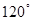 ,则以
,则以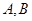 为焦点且过点
为焦点且过点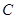 的双曲线的离心率为
的双曲线的离心率为 A. | B. | C. | D. |
B 由题意知设焦距为2c,则|AB|=2c,|BC|=2c,则|AC|=2|AB|cos30°=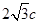 ,
,
所以由双曲线的定义知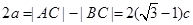 ,
,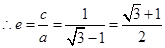 ,故选B.
,故选B.
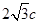 ,
,所以由双曲线的定义知
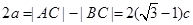 ,
,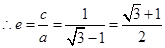 ,故选B.
,故选B.分析:根据题设条件可知2c=|BC|,所以|AC|=2×2c×sin600="2"
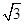 c,由双曲线的定义能够求出2a,从而导出双曲线的离心率.
c,由双曲线的定义能够求出2a,从而导出双曲线的离心率.解:由题意2c=|BC|,所以|AC|=2×2c×sin600=2
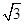 c,由双曲线的定义,有2a=|AC|-|BC|=2
c,由双曲线的定义,有2a=|AC|-|BC|=2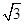 c-2c?a=(
c-2c?a=(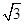 -1)c,
-1)c,∴
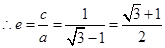
故选B.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
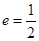 ,过左焦点
,过左焦点 作直线
作直线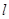 与椭圆交于点P,Q,直线AP,AQ分别与直线
与椭圆交于点P,Q,直线AP,AQ分别与直线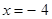 交于点
交于点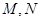 .
.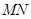 为直径的圆经过焦点
为直径的圆经过焦点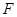 .
. ,直线
,直线 过椭圆左焦点
过椭圆左焦点 且不与
且不与 轴重合,
轴重合,  ,两点,当
,两点,当 ,若点
,若点 且
且
 的方程;
的方程; 交于
交于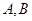 两点,若
两点,若 ,求
,求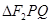 的面积
的面积 的取值范围(
的取值范围( 为椭圆的右焦点)。
为椭圆的右焦点)。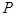 是椭圆
是椭圆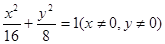 上的动点,
上的动点,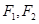 为椭圆的两个焦点,
为椭圆的两个焦点,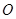 是坐标原点,若
是坐标原点,若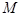 是
是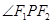 的角平分线上一点,且
的角平分线上一点,且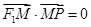 ,则
,则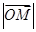 的取值范围是( )
的取值范围是( )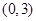
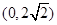
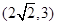
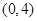
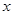 轴上,离心率为
轴上,离心率为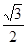 ,它与直线
,它与直线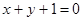 相交于P、Q两点,若
相交于P、Q两点,若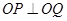 ,求椭圆方程。
,求椭圆方程。 的左、右焦点,点P在椭圆上,且
的左、右焦点,点P在椭圆上,且 记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1: 2,则该椭圆的离心率等于 ( )
记线段PF1与y轴的交点为Q,O为坐标原点,若△F1OQ与四边形OF2PQ的面积之比为1: 2,则该椭圆的离心率等于 ( )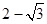
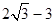

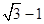
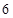 ,短轴长为8,
,短轴长为8,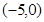 作倾斜角为
作倾斜角为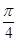 的直线交椭圆C于A、B两点,求
的直线交椭圆C于A、B两点,求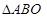 的面积。
的面积。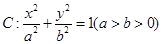 的离心率为
的离心率为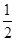 ,直线
,直线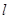 过点
过点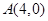 ,
,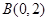 ,且与椭圆
,且与椭圆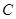 相切于点
相切于点 .
. 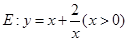 相交于不同的两点
相交于不同的两点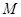 、
、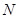 ,曲线
,曲线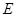 在点
在点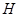 .试问:点
.试问:点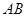 是椭圆
是椭圆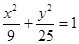 的不垂直于对称轴的弦,
的不垂直于对称轴的弦,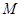 为
为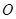 为坐标原点,则
为坐标原点,则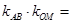 ____________
____________