题目内容
中心点在原点,准线方程为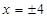 ,离心率为
,离心率为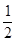 的椭圆方程是( )
的椭圆方程是( )
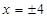 ,离心率为
,离心率为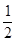 的椭圆方程是( )
的椭圆方程是( )A. | B. | C.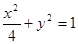 | D.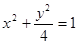 |
A
由条件可设椭圆方程为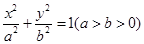 ,则
,则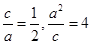 ,解得a=2,
,解得a=2,
C=1,所以b=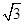 .故选A
.故选A
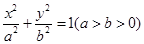 ,则
,则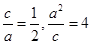 ,解得a=2,
,解得a=2,C=1,所以b=
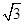 .故选A
.故选A
练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
题目内容
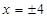 ,离心率为
,离心率为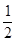 的椭圆方程是( )
的椭圆方程是( )A. | B. | C.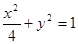 | D.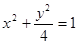 |
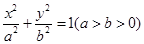 ,则
,则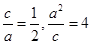 ,解得a=2,
,解得a=2,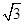 .故选A
.故选A
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案