题目内容
17．在区间[-2，1]任取两个实数x，y，则x+y＞0概率为（ ）| A． | $\frac{2}{9}$ | B． | $\frac{4}{9}$ | C． | $\frac{1}{2}$ | D． | $\frac{7}{9}$ |
分析 该题涉及两个变量，故是与面积有关的几何概型，分别表示出满足条件的面积和整个区域的面积，最后利用概率公式解之即可．
解答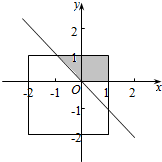 
解：由题意可得，区域为边长为3的正方形，面积为9，
满足x+y＞0的区域为图中阴影部分，面积为$\frac{1}{2}×2×2$=2，
由几何概型公式可得x+y＞0概率为$\frac{2}{9}$；
故选：A．
点评 本题主要考查了与面积有关的几何概率的求解，解题的关键是准确求出区域的面积，属于中档题．
练习册系列答案
快捷英语周周练系列答案
相关题目
扣人心弦的2014巴西足球世界杯已落下了帷幕，德国战车再次举起大力神杯，某市足协为了解市民对该届世界杯的关注度，针对某种与世界杯有关的吉祥物的销售情况组织了一次随机调查，以下是某商店根据以往某种吉祥物的销售记录绘制的频率分布直方图，如图所示．将日销售量落入各组的频率视为概率，并假设每天的销售量相互独立．
5．已知集合$A=\{x|y=\sqrt{{{log}_2}x}\}，B=\{y|y=\frac{1}{2^x}，x＞0\}$，则A∩CRB=（ ）
| A． | （0，1） | B． | （-∞，1] | C． | [1，+∞） | D． | φ |
12．已知圆（x-a）2+（y-b）2=1与两直线l1：3x-4y-1=0和l2：4x+3y+1=0都有公共点，则$\frac{b}{a+2}$的取值范围为（ ）
| A． | [-$\frac{1}{2}$，$\frac{1}{4}$] | B． | [$\frac{1}{4}$，$\frac{3}{4}$] | C． | （-∞，-$\frac{1}{2}$]∪[$\frac{3}{4}$，+∞） | D． | [-$\frac{21}{22}$，$\frac{14}{27}$] |
2．某校为了解高三年级不同性别的学生对取消艺术课的态度（支持或反对），进行了如下的调查研究．全年级共有1350人，男女生比例为8：7，现按分层抽样方法抽取若干名学生，每人被抽到的概率均为$\frac{1}{9}$，通过对被抽取学生的问卷调查，得到如下2x2列联表：
（I）完成列联表，并判断能否有99.9%的把握认为态度与性别有关？
（皿）若某班有6名男生被抽到，其中2人支持，4人反对；有4名女生被抽到，其中2人支持，2人反对，现从这10人中随机抽取一男一女进一步调查原因．求其中恰有一人支持一人反对的概率．
参考公式及临界表：K2=$\frac{n（ad-bc）^{2}}{（a+c）（b+d）（a+b）（c+d）}$
| 支持 | 反对 | 总计 | |
| 男生 | 30 | ||
| 女生 | 25 | ||
| 总计 |
（皿）若某班有6名男生被抽到，其中2人支持，4人反对；有4名女生被抽到，其中2人支持，2人反对，现从这10人中随机抽取一男一女进一步调查原因．求其中恰有一人支持一人反对的概率．
参考公式及临界表：K2=$\frac{n（ad-bc）^{2}}{（a+c）（b+d）（a+b）（c+d）}$
| P（K2≥k0） | 0.10 | 0.050 | 0.010 | 0.005 | 0.001 |
| k0 | 2.706% | 3.841 | 6.635 | 7.879 | 10.828 |
9．要得到函数y=sin（x+$\frac{π}{6}$）的图象，只需要将函数y=cosx的图象（ ）
| A． | 向左平移$\frac{π}{3}$个单位 | B． | 向左平移$\frac{π}{6}$个单位 | ||
| C． | 向右平移$\frac{π}{3}$个单位 | D． | 向右平移$\frac{π}{6}$个单位 |
6．已知函数f（x-1）的定义域是（1，2），那么f（2x）的定义域是（ ）
| A． | （0，1） | B． | （$\frac{1}{2}$，1） | C． | （-∞，0） | D． | （0，+∞） |