题目内容
8.函数y=cos2x+2cosx的最大值为3.分析 由cos2x=2cos2x-1,利用配方法得到y=cos2x+2cosx=2(cosx+$\frac{1}{2}$)2-$\frac{3}{2}$,由此能求出函数y=cos2x+2cosx的最大值.
解答 解:∵y=cos2x+2cosx
=2cos2x+2cosx-1
=2(cosx+$\frac{1}{2}$)2-$\frac{3}{2}$,
∴当cosx=1时,函数y=cos2x+2cosx取最大值ymax=2(1+$\frac{1}{2}$)2-$\frac{3}{2}$=3.
故答案为:3.
点评 本题考查三角函数的最大值的求法,是基础题,解题时要认真审题,注意三角函数的性质的合理运用.

练习册系列答案
相关题目
19.在如图的程序框图中,若输入的值为2,则输出的值为( )
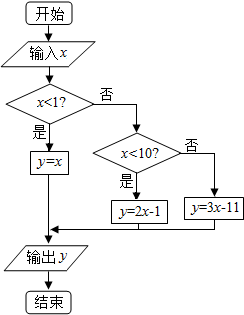

| A. | 2 | B. | 3 | C. | -5 | D. | 6 |
13.数列{an}中,满足an+2=2an+1-an,且a1,a4031是函数f(x)=$\frac{1}{3}{x^3}-4{x^2}+6x-1$的极值点,则log2a2016的值是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
17.在区间[-2,1]任取两个实数x,y,则x+y>0概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{9}$ |
18.设集合A={a,b},则满足A∪B={a,b,c}的集合B的个数为( )
| A. | 8 | B. | 4 | C. | 3 | D. | 1 |
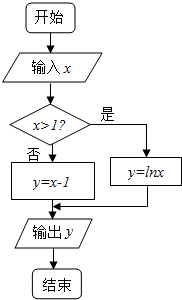 某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.
某算法的程序框图如图所示,则输出量y与输入量x满足的关系式是y=$\left\{\begin{array}{l}x-1,x≤1\\ lnx,x>1\end{array}\right.$.