题目内容
9.要得到函数y=sin(x+$\frac{π}{6}$)的图象,只需要将函数y=cosx的图象( )| A. | 向左平移$\frac{π}{3}$个单位 | B. | 向左平移$\frac{π}{6}$个单位 | ||
| C. | 向右平移$\frac{π}{3}$个单位 | D. | 向右平移$\frac{π}{6}$个单位 |
分析 由条件利用诱导公式以及y=Asin(ωx+φ)的图象变换规律,可得结论.
解答 解:将函数y=cosx的图象向右平移$\frac{π}{3}$个单位,
可得y=cos(x-$\frac{π}{3}$)=sin(x-$\frac{π}{3}$+$\frac{π}{2}$)=sin(x+$\frac{π}{6}$)的图象,
故选:C.
点评 本题主要考查诱导公式的应用,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
19.在如图的程序框图中,若输入的值为2,则输出的值为( )
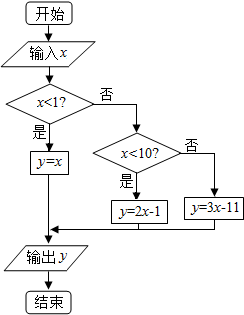

| A. | 2 | B. | 3 | C. | -5 | D. | 6 |
17.在区间[-2,1]任取两个实数x,y,则x+y>0概率为( )
| A. | $\frac{2}{9}$ | B. | $\frac{4}{9}$ | C. | $\frac{1}{2}$ | D. | $\frac{7}{9}$ |
4.已知角α终边上一点P的坐标是(2sin2,-2cos2),则sinα等于( )
| A. | sin2 | B. | -sin2 | C. | cos2 | D. | -cos2 |
1.函数f(x)是定义在R上偶函数,当x≥0时,f(x)单调递减.则下列各式成立的是( )
| A. | f(1)<f(-3) | B. | f(3)>f(2) | C. | f(-2)>f(3) | D. | f(2)>f(0) |
18.设集合A={a,b},则满足A∪B={a,b,c}的集合B的个数为( )
| A. | 8 | B. | 4 | C. | 3 | D. | 1 |