题目内容
【题目】如图所示,在矩形ABCD中,AB=3![]() ,BC=3,沿对角线BD将△BCD折起,使点C移到C′点,且C′点在平面ABD上的射影O恰在AB上.
,BC=3,沿对角线BD将△BCD折起,使点C移到C′点,且C′点在平面ABD上的射影O恰在AB上.
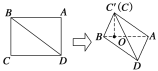
(1)求证:BC′⊥平面AC′D;
(2)求点A到平面BC′D的距离.
【答案】(1)详见解析(2)![]()
【解析】
(1)由题设可得![]() 平面
平面![]() ,从可得
,从可得![]() ,再根据
,再根据![]() 可得
可得![]() 平面
平面![]() ,故可得
,故可得![]() ,结合
,结合![]() 可得要证明的线面垂直.
可得要证明的线面垂直.
(2)过![]() 作
作![]() 交
交![]() 于
于![]() ,可证
,可证![]() 为
为![]() 到平面
到平面![]() 的距离,最后利用
的距离,最后利用![]() 得到
得到![]() 的长.
的长.
(1)证明 ∵点![]() 在平面
在平面![]() 上的射影
上的射影![]() 在
在![]() 上,
上,
∴![]() 平面
平面![]() ,
,![]() 平面
平面![]() , ∴
, ∴![]() .
.
又∵![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() , ∴
, ∴![]() .
.
又∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)
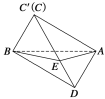
如图所示,过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() , ∴
, ∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() .
.
故![]() 的长就是
的长就是![]() 点到平面
点到平面![]() 的距离.
的距离.
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() 平面
平面![]() ,又
,又![]() 平面
平面![]() , ∴
, ∴![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,
中,![]() .
.
在![]() 中,由面积关系,得
中,由面积关系,得
![]() .
.
∴点![]() 到平面
到平面![]() 的距离是
的距离是![]() .
.

练习册系列答案
相关题目