��Ŀ����
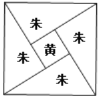
����Ŀ������ʱ�������ѧ����ˬ��ע�������㾭���и����˹��ɶ����ľ���֤��.��������ˬ����ͼ��ע�ģ���ͼ��һ���Թ�����֮��Ϊ�ߵ������Σ��������Ϊ��ʵ��ͼ�а����ĸ�ȫ�ȵĹ����μ�һ��С�����Σ��ֱ�Ϳ�ɺ죨�죩ɫ����ɫ���������Ϊ��ʵ��ʵ������![]() ��
��![]() ��
��![]() ����
����![]() ����
����![]() ��ʵ
��ʵ![]() ��ʵ
��ʵ![]() ��ʵ�����ù�
��ʵ�����ù�![]() ��
��![]() ��
��![]() ���蹴���й��ɱ�Ϊ
���蹴���й��ɱ�Ϊ![]() ��������ͼ���������
��������ͼ���������![]() ��ͼ������С���Բ��ƣ��������ڻ�ɫͼ���ڵ�ͼ��������ԼΪ�� �����ο�����
��ͼ������С���Բ��ƣ��������ڻ�ɫͼ���ڵ�ͼ��������ԼΪ�� �����ο�����![]() ��
��![]() ��
��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
���𰸡�B
��������
��������,����̱߹��ij�Ϊ![]() ,������ʾ���ɺ���,���С��������������ε������,��ϼ��θ��������ɵý�.
,������ʾ���ɺ���,���С��������������ε������,��ϼ��θ��������ɵý�.
��������,������̱߹��ij�Ϊ![]()
���Ϊ![]() ,��Ϊ
,��Ϊ![]()
���Դ������ε����Ϊ![]()
С�����ε����Ϊ![]()
��С��������������ε������Ϊ
�ɼ��θ����ʼ��㷽���ɵ�
�������ڻ�ɫͼ���ڵ�ͼ��������ԼΪ![]() ��
��
��ѡ:B

��ϰ��ϵ�д�
�����Ŀ