题目内容
【题目】某车间为了规定工时额定,需要确定加工零件所花费的时间,为此作了![]() 次试验,得到数据如下:
次试验,得到数据如下:
零件数 | 10 | 20 | 30 | 40 | 50 | 60 |
加工时间 | 64 | 70 | 77 | 82 | 90 | 97 |
(1)试对上述变量![]() 与
与![]() 的关系进行相关性检验,如果
的关系进行相关性检验,如果![]() 与
与![]() 具有线性相关关系,求出
具有线性相关关系,求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)根据(1)的结论,你认为每小时加工零件的数量额定为多少(四舍五入为整数)比较合理?
附:相关性检验的临界值表
| 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
4 | 0.811 | 0.917 |
5 | 0.754 | 0.874 |
6 | 0.707 | 0.834 |
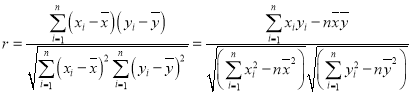
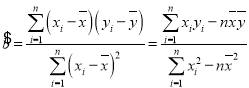 ,
,![]()
参考数据:![]() ;
;![]()
|
|
|
|
|
17950 | 9100 | 39158 | 1750 | 758 |
【答案】(1)答案见解析.(2)![]()
【解析】
(1)根据表中所给数据,计算出![]() ,即可求得答案.
,即可求得答案.
(2)每小时加工零件的数量,即![]() ,将
,将![]() 代入
代入![]() ,即可求得答案.
,即可求得答案.
(1)由表中数据得:![]() ,
,![]() ,
,![]() ,
,![]()
![]()
![]()
从而有95%的把握认为![]() 与
与![]() 之间具有线性相关关系,
之间具有线性相关关系,
![]() 此求回归直线方程是有意义的.
此求回归直线方程是有意义的.
计算得:![]()
![]()
![]()
(2)![]() 每小时加工零件的数量,即
每小时加工零件的数量,即![]()
将![]() 代入
代入![]()
![]()
故每小时加工零件的数量额定为![]() 比较合理
比较合理

练习册系列答案
相关题目