题目内容
【题目】十九大以来,国家深入推进精准脱贫,加大资金投入,强化社会帮扶,为了更好的服务于人民,派调查组到某农村去考察和指导工作.该地区有100户农民,且都从事水果种植,据了解,平均每户的年收入为2万元.为了调整产业结构,调查组和当地政府决定动员部分农民从事水果加工,据估计,若能动员![]() 户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高
户农民从事水果加工,则剩下的继续从事水果种植的农民平均每户的年收入有望提高![]() ,而从事水果加工的农民平均每户收入将为
,而从事水果加工的农民平均每户收入将为![]() 万元.
万元.
(1)若动员![]() 户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求
户农民从事水果加工后,要使从事水果种植的农民的总年收入不低于动员前从事水果种植的农民的总年收入,求![]() 的取值范围;
的取值范围;
(2)在(1)的条件下,要使这100户农民中从事水果加工的农民的总收入始终不高于从事水果种植的农民的总收入,求![]() 的最大值.
的最大值.
【答案】(1)![]() <
<![]() (2)最大值为9
(2)最大值为9
【解析】
(1)由题意写出不等关系,解不等式即可得解;
(2)由题意写出不等关系,分离参数得![]() ,利用基本不等式求出
,利用基本不等式求出![]() 的最小值即可得解.
的最小值即可得解.
(1)由题意![]()
![]() 得
得![]() ,
,
由![]() 可得
可得![]() .
.
答:![]() 的取值范围为
的取值范围为![]() .
.
(2)由题意得![]() ,
,
所以![]() 在
在![]() 上恒成立,
上恒成立,
又 ![]() ,(当且仅当
,(当且仅当![]() 时取“=”),
时取“=”),
所以![]() .
.
答:![]() 的最大值为9.
的最大值为9.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
【题目】某车间为了规定工时额定,需要确定加工零件所花费的时间,为此作了![]() 次试验,得到数据如下:
次试验,得到数据如下:
零件数 | 10 | 20 | 30 | 40 | 50 | 60 |
加工时间 | 64 | 70 | 77 | 82 | 90 | 97 |
(1)试对上述变量![]() 与
与![]() 的关系进行相关性检验,如果
的关系进行相关性检验,如果![]() 与
与![]() 具有线性相关关系,求出
具有线性相关关系,求出![]() 对
对![]() 的回归直线方程;
的回归直线方程;
(2)根据(1)的结论,你认为每小时加工零件的数量额定为多少(四舍五入为整数)比较合理?
附:相关性检验的临界值表
| 小概率 | |
0.05 | 0.01 | |
3 | 0.878 | 0.959 |
4 | 0.811 | 0.917 |
5 | 0.754 | 0.874 |
6 | 0.707 | 0.834 |
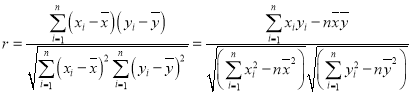
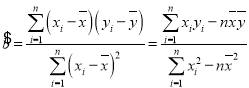 ,
,![]()
参考数据:![]() ;
;![]()
|
|
|
|
|
17950 | 9100 | 39158 | 1750 | 758 |