Question

【题目】某工厂有两台不同机器A和B生产同一种产品各10万件,现从各自生产的产品中分别随机抽取二十件，进行品质鉴定，鉴定成绩的茎叶图如下所示：

该产品的质量评价标准规定：鉴定成绩达到的产品，质量等级为优秀；鉴定成绩达到的产品，质量等级为良好；鉴定成绩达到的产品，质量等级为合格．将这组数据的频率视为整批产品的概率．

（1）从等级为优秀的样本中随机抽取两件，记为来自B机器生产的产品数量，写出的分布列，并求的数学期望；

（2）完成下列列联表，以产品等级是否达到良好以上（含良好）为判断依据，判断能不能在误差不超过0.05的情况下，认为B机器生产的产品比A机器生产的产品好；

	A生产的产品	B生产的产品	合计
良好以上（含良好）
合格
合计

（3）已知优秀等级产品的利润为12元/件，良好等级产品的利润为10元/件，合格等级产品的利润为5元/件，A机器每生产10万件的成本为20万元，B机器每生产10万件的成本为30万元；该工厂决定：按样本数据测算，两种机器分别生产10万件产品，若收益之差达到5万元以上，则淘汰收益低的机器，若收益之差不超过5万元，则仍然保留原来的两台机器.你认为该工厂会仍然保留原来的两台机器吗？

Answer 1

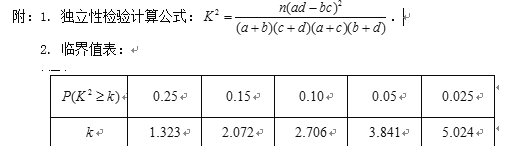
【答案】（1）见解析；（2）见解析；（3）见解析

【解析】分析：（1）先计算出样本中优秀的产品有2个来自A机器，3个来自B 机器，再写出x的分布列和期望. (2)先完成2×2列联表，再求出作出判断.(3)先计算出A、B机器每生产10万件的利润,再下结论.

详解：（1）从茎叶图可以知道，样本中优秀的产品有2个来自A机器，3个来自B 机器；

所以的可能取值为．

，，．

的分布列为：

	0	1	2
	0.1	0.6	0.3

所以．

（2）由已知可得，列联表为

	A生产的产品	B生产的产品	合计
良好以上	6	12	18
合格	14	8	22
合计	20	20	40

，

所以不能在误差不超过0.05的情况下，认为产品等级是否达到良好以上与生产产品的机器有关．

（3）A机器每生产10万件的利润为万元，

B机器每生产10万件的利润为万元，

所以，

所以该工厂不会仍然保留原来的两台机器，应该会卖掉A机器，同时购买一台B机器．