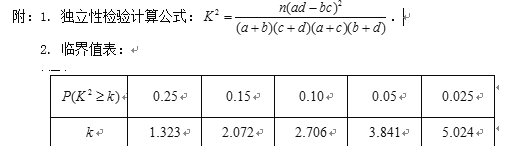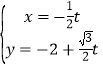题目内容
【题目】已知椭圆![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,
,![]() 为椭圆上不与左右顶点重合的任意一点,
为椭圆上不与左右顶点重合的任意一点,![]() ,
,![]() 分别为
分别为![]() 的内心、重心,当
的内心、重心,当![]() 轴时,椭圆的离心率为( )
轴时,椭圆的离心率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
结合图像,利用![]() 点坐标以及重心性质,得到G点坐标,再由题目条件
点坐标以及重心性质,得到G点坐标,再由题目条件![]() 轴,得到
轴,得到![]() 点横坐标,然后两次运用角平分线的相关性质得到
点横坐标,然后两次运用角平分线的相关性质得到![]() 的比值,再结合
的比值,再结合![]() 与
与![]() 相似,即可求得
相似,即可求得![]() 点纵坐标,也就是内切圆半径,再利用等面积法建立关于
点纵坐标,也就是内切圆半径,再利用等面积法建立关于![]() 的关系式,从而求得椭圆离心率.
的关系式,从而求得椭圆离心率.
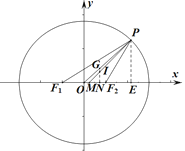
如图,令![]() 点在第一象限(由椭圆对称性,其他位置同理),连接
点在第一象限(由椭圆对称性,其他位置同理),连接![]() ,显然
,显然![]() 点在
点在![]() 上,连接
上,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,连接
,连接![]() 并延长交
并延长交![]() 轴于点
轴于点![]() ,
,![]() 轴,过点
轴,过点![]() 作
作![]() 垂直于
垂直于![]() 轴于点
轴于点![]() ,
,
设点![]() ,
,![]() ,则
,则![]() ,
,
因为![]() 为
为![]() 的重心,所以
的重心,所以![]() ,
,
因为![]() 轴,所以
轴,所以![]() 点横坐标也为
点横坐标也为![]() ,
,![]() ,
,
因为![]() 为
为![]() 的角平分线,
的角平分线,
则有![]() ,
,
又因为![]() ,所以可得
,所以可得![]() ,
,
又由角平分线的性质可得,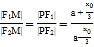 ,而
,而![]()
所以得![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ,即
,即![]() ,
,
因为![]()
即![]() ,解得
,解得![]() ,所以答案为A.
,所以答案为A.

【题目】2018年4月4日召开的国务院常务会议明确将进一步推动网络提速降费工作落实,推动我国数字经济发展和信息消费,今年移动流量资费将再降![]() 以上,为响应国家政策,某通讯商计划推出两款优惠流量套餐,详情如下:
以上,为响应国家政策,某通讯商计划推出两款优惠流量套餐,详情如下:
套餐名称 | 月套餐费/元 | 月套餐流量/M |
A | 30 | 3000 |
B | 50 | 6000 |
这两款套餐均有以下附加条款:套餐费用月初一次性收取,手机使用流量一旦超出套餐流量,系统就会自动帮用户充值![]() 流量,资费20元;如果又超出充值流量,系统再次自动帮用户充值
流量,资费20元;如果又超出充值流量,系统再次自动帮用户充值![]() 流量,资费20元,以此类推.此外,若当月流量有剩余,系统将自动清零,不可次月使用.
流量,资费20元,以此类推.此外,若当月流量有剩余,系统将自动清零,不可次月使用.
小张过去50个月的手机月使用流量(单位:M)的频数分布表如下:
月使用流量分组 |
|
|
|
|
|
|
频数 | 4 | 5 | 11 | 16 | 12 | 2 |
根据小张过去50个月的手机月使用流量情况,回答以下几个问题:
(1)若小张选择A套餐,将以上频率作为概率,求小张在某一个月流量费用超过50元的概率;
(2)小张拟从A或B套餐中选定一款,若以月平均费用作为决策依据,他应订哪一种套餐?说明理由.
【题目】某工厂有两台不同机器A和B生产同一种产品各10万件,现从各自生产的产品中分别随机抽取二十件,进行品质鉴定,鉴定成绩的茎叶图如下所示:

该产品的质量评价标准规定:鉴定成绩达到![]() 的产品,质量等级为优秀;鉴定成绩达到
的产品,质量等级为优秀;鉴定成绩达到![]() 的产品,质量等级为良好;鉴定成绩达到
的产品,质量等级为良好;鉴定成绩达到![]() 的产品,质量等级为合格.将这组数据的频率视为整批产品的概率.
的产品,质量等级为合格.将这组数据的频率视为整批产品的概率.
(1)从等级为优秀的样本中随机抽取两件,记![]() 为来自B机器生产的产品数量,写出
为来自B机器生产的产品数量,写出![]() 的分布列,并求
的分布列,并求![]() 的数学期望;
的数学期望;
(2)完成下列![]() 列联表,以产品等级是否达到良好以上(含良好)为判断依据,判断能不能在误差不超过0.05的情况下,认为B机器生产的产品比A机器生产的产品好;
列联表,以产品等级是否达到良好以上(含良好)为判断依据,判断能不能在误差不超过0.05的情况下,认为B机器生产的产品比A机器生产的产品好;
A生产的产品 | B生产的产品 | 合计 | |
良好以上(含良好) | |||
合格 | |||
合计 |
(3)已知优秀等级产品的利润为12元/件,良好等级产品的利润为10元/件,合格等级产品的利润为5元/件,A机器每生产10万件的成本为20万元,B机器每生产10万件的成本为30万元;该工厂决定:按样本数据测算,两种机器分别生产10万件产品,若收益之差达到5万元以上,则淘汰收益低的机器,若收益之差不超过5万元,则仍然保留原来的两台机器.你认为该工厂会仍然保留原来的两台机器吗?