题目内容
【题目】设函数f(x)=ax3-3ax,g(x)=bx2-ln x(a,b∈R),已知它们在x=1处的切线互相平行.
(1)求b的值;
(2)若函数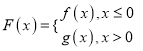 且方程F(x)=a2有且仅有四个解,求实数a的取值范围.
且方程F(x)=a2有且仅有四个解,求实数a的取值范围.
【答案】(1)![]() ;(2)
;(2)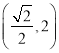
【解析】试题分析:(1)由![]() 和
和![]() 在
在![]() 处的切线互相平行得,
处的切线互相平行得, ![]() ,解方程求出
,解方程求出![]() 值.
值.
(2)分别求出求出![]() 的极值和
的极值和![]() 的极值,结合单调性画出
的极值,结合单调性画出![]() 的图象,结合图象可得若方程
的图象,结合图象可得若方程![]() 有四个解,则
有四个解,则 ![]() ,解不等式求得实数
,解不等式求得实数![]() 的取值范围.
的取值范围.
试题解析:函数g(x)=bx2-ln x的定义域为(0,+∞),
(1)f′(x)=3ax2-3af′(1)=0,
g′(x)=2bx-![]() g′(1)=2b-1,
g′(1)=2b-1,
依题意得2b-1=0,所以b=![]() .
.
(2)x∈(0,1)时,g′(x)=x-![]() <0,
<0,
即g(x)在(0,1)上单调递减,
x∈(1,+∞)时,g′(x)=x-![]() >0,即g(x)在(1,+∞)上单调递增,所以当x=1时,g(x)取得极小值g(1)=
>0,即g(x)在(1,+∞)上单调递增,所以当x=1时,g(x)取得极小值g(1)=![]() ;当a=0时,方程F(x)=a2不可能有四个解;
;当a=0时,方程F(x)=a2不可能有四个解;
当a<0,x∈(-∞,-1)时,f′(x)<0,即f(x)在(-∞,-1)上单调递减,x∈(-1,0)时,f′(x)>0,
即f(x)在(-1,0)上单调递增,
所以当x=-1时,f(x)取得极小值f(-1)=2a,
又f(0)=0,所以F(x)的图象如图①所示,

从图象可以看出F(x)=a2不可能有四个解.
当a>0,x∈(-∞,-1)时,f′(x)>0,
即f(
x∈(-1,0)时,f′(x)<0,
即f(x)在(-1,0)上单调递减,
所以当x=-1时,f(x)取得极大值f(-1)=2a.又f(0)=0,所以F(x)的图象如图②所求,

从图②看出,若方程F(x)=a2有四个解,则![]() <a2<2a,
<a2<2a,
得![]() <a<2,
<a<2,
所以,实数a的取值范围是![]() .
.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案【题目】为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99%的把握认为“喜爱打篮球与性别有关”?说明你的理由.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|