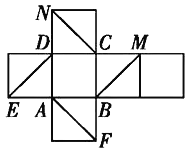
题目内容
【题目】如图所示是一个正方体的平面展开图,在这个正方体中![]() 平面ADE;
平面ADE;![]() 平面ABF;
平面ABF;![]() 平面
平面![]() 平面AFN;
平面AFN;![]() 平面
平面![]() 平面NCF.以上四个命题中,真命题的序号是
平面NCF.以上四个命题中,真命题的序号是![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】
把正方体的平面展开图还原成正方体ABCA﹣EFMN,得出BM∥平面ADNE,判断①正确;由平面DCMN∥平面ABFE,得出CN∥平面ABFE,判断②正确;由BD∥FN,得出BD∥平面AFN,同理BM∥平面AFN,证明平面BDM∥平面AFN,判断③正确;由BD∥FN,BE∥CN,且BD∩BE=B,证明平面BDE∥平面NCF,判断④正确.
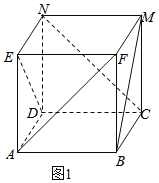
把正方体的平面展开图还原成正方体ABCA﹣EFMN,如图1所示;
对于①,平面BCMF∥平面ADNE,BM平面BCMF,
∴BM∥平面ADNE,①正确;
对于②,平面DCMN∥平面ABFE,CN平面DCMN,
∴CN∥平面ABFE,②正确;
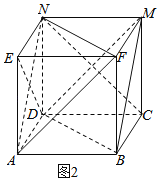
对于③,如图2所示,
BD∥FN,BD平面AFN,FN平面AFN,∴BD∥平面AFN;
同理BM∥平面AFN,且BD∩BM=B,
∴平面BDM∥平面AFN,③正确;
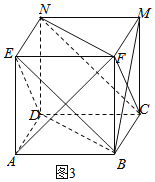
对于④,如图3所示,
BD∥FN,BE∥CN,BD∩BE=B,且BD、BE平面BDE,
∴平面BDE∥平面NCF,∴④正确.
综上,正确的命题序号是![]() .
.
故答案为:A.

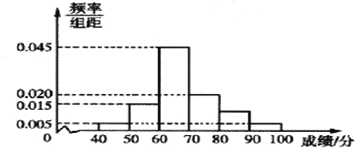
【题目】节能灯的质量通过其正常使用时间来衡量,使用时间越长,表明质量越好,且使用时间大于或等于6千小时的产品为优质品.现用A,B两种不同型号的节能灯做试验,各随机抽取部分产品作为样本,得到试验结果的频率分布直方图如图所示.
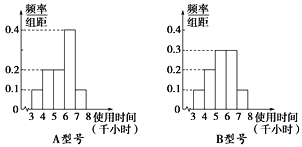
以上述试验结果中使用时间落入各组的频率作为相应的概率.
(1)现从大量的A,B两种型号节能灯中各随机抽取两件产品,求恰有两件是优质品的概率;
(2)已知A型节能灯的生产厂家对使用时间小于6千小时的节能灯实行“三包”.通过多年统计发现,A型节能灯每件产品的利润y(单位:元)与其使用时间t(单位:千小时)的关系如下表:
使用时间t(单位:千小时) | t<4 | 4≤t<6 | t≥6 |
每件产品的利润y(单位:元) | -10 | 10 | 20 |
若从大量的A型节能灯中随机抽取两件,其利润之和记为X(单位:元),求X的分布列及数学期望.