题目内容
【题目】为了解某班学生喜爱打篮球是否与性别有关，对本班50人进行了问卷调查得到了如下的列联表：
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 5 | ||
女生 | 10 | ||
合计 | 50 |
已知在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
．
（1）请将上面的列联表补充完整；
（2）是否有99%的把握认为“喜爱打篮球与性别有关”？说明你的理由．
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【答案】（1）见解析； （2）有99%的把握认为“喜爱打篮球与性别有关”．
【解析】
（1）利用题干中所给的条件即可求出填表即可；
（2）求出
,然后判断是否有99%的把握认为“喜爱打篮球与性别有关”。
（1）因为在全部50人中随机抽取1人抽到喜爱打篮球的学生的概率为
，
所以喜爱打篮球的总人数为
人，
所以补充完整的
列联表如下：
喜爱打篮球 | 不喜爱打篮球 | 合计 | |
男生 | 15 | 5 | 20 |
女生 | 10 | 20 | 30 |
合计 | 25 | 25 | 50 |
（2）根据列联表可得的观测值
，
所以有99%的把握认为“喜爱打篮球与性别有关”．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
【题目】设函数f(x)＝ax3－3ax，g(x)＝bx2－ln x(a，b∈R)，已知它们在x＝1处的切线互相平行.
(1)求b的值；
(2)若函数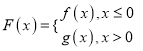
且方程F(x)＝a2有且仅有四个解，求实数a的取值范围.
【题目】某幼儿园雏鹰班的生活老师统计2018年上半年每个月的20日的昼夜温差
，
和患感冒的小朋友人数（
/人）的数据如下：
温差 |
|
|
|
|
|
|
患感冒人数 | 8 | 11 | 14 | 20 | 23 | 26 |
其中
，
，
.
（Ⅰ）请用相关系数加以说明是否可用线性回归模型拟合与
（Ⅱ）建立关于
的回归方程（精确到
），预测当昼夜温差升高
时患感冒的小朋友的人数会有什么变化？（人数精确到整数）
参考数据：
．参考公式：相关系数：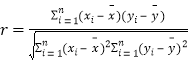
，回归直线方程是
，
,
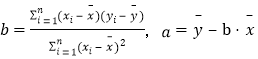