题目内容
2.已知y=f(x)是定义在R上的偶函数,当x≥0时,f(x)=x2-2x(1)求f(1),f(-2)的值;
(2)求f(x)的解析式;
(3)讨论方程f(x)=k的根的情况.(只需写出结果,不要解答过程).
分析 (1)由函数为偶函数可知f(-2)=f(2),根据已知条件易求出f(1),f(2);
(2)利用函数的奇偶性易求出函数的解析式,并画出图象;
(3)方程f(x)=k的根的情况就是函数y=f(x)的图象与函数y=k的图象的交点的情况,由图象易分析出交点的个数,得到问题的解.
解答 解:(1)f(1)=12-2•1=-1.
∵y=f(x)是定义在R上的偶函数,
∴f(-2)=f(2)=22-2•2=0…(3分)
(2)当x≤0时,-x≥0,于是f(-x)=(-x)2-2(-x)=x2+2x
∵y=f(x)是定义在R上的偶函数,
∴f(x)=f(-x)=x2+2x(x≤0)
∴$f(x)=\left\{{\begin{array}{l}{{x^2}-2x(x>0)}\\{{x^2}+2x(x≤0)}\end{array}}\right.$…(8分)
画出简图(如图) 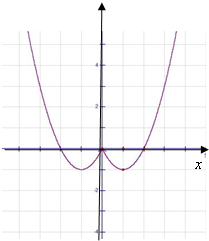
(3)当k<-1,方程无实根
当k=-1或k>0,有2个实数根;
当k=0,有3个实数根;
当-1<k<0,有4个实数根…(12分)
点评 本题考查函数的性质与应用,考查函数的解析式,考查数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
13.不等式x2-4x-5<0 的解集为( )
| A. | {x|-1<x<5} | B. | {x|-5<x<1} | C. | {x|x>5或x<-1} | D. | {x|x>1或x<-5} |
7.若正数m,n满足m+3n=5mn,则3m+4n的最小值为( )
| A. | $\frac{24}{5}$ | B. | $\frac{28}{5}$ | C. | 6 | D. | 5 |
11.一名大毕业生,准备利用上学期间打工积攒下来的钱去投资甲、乙两个网站,投资金额不超过10万元,有信息表明这两个网店既可能盈利,也可能亏损,盈利率(盈利率=$\frac{盈利额}{投资额}$)和亏损率(亏损率=$\frac{亏损额}{投资额}$),如表所示:
该大学生在确保总的亏损额不超过2.4万元的情况下,为了获得最大盈利,应投资甲、乙两个网店各多少万元?最大盈利是多少万元?
| 盈利率 | 亏损率 | |
| 甲网店 | 60% | 30% |
| 乙网店 | 40% | 15% |
 如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面为S.则下列命题正确的是①②④(写出所有正确命题的编号).
如图,正方体ABCD-A1B1C1D1的棱长为1,P为BC的中点,Q为线段CC1上的动点,过点A,P,Q的平面截该正方体所得的截面为S.则下列命题正确的是①②④(写出所有正确命题的编号).