题目内容
5.若方程x2+ax+2b=0的一个根在(0,1)内,另一个根在(1,2)内,则$\frac{b-a}{a-1}$的取值范围是(-1,-$\frac{1}{2}$).分析 设f(x)=x2+ax+2b,根据二次函数的性质与零点存在性定理可得f(0)>0、f(1)<0且f(2)>0.由此建立关于a、b的二元一次不等式组,设点E(a,b)为区域内的任意一点,则$\frac{b-a}{a-1}$=$\frac{b-1}{a-1}$-1,k=$\frac{b-1}{a-1}$,根据直线的斜率公式可得k=$\frac{b-1}{a-1}$,表示D(1,1)、E连线的斜率,将点E在区域内运动并观察直线的倾斜角的变化,即可算出$\frac{b-a}{a-1}$的取值范围.
解答 解:设f(x)=x2+ax+2b,
∵方程x2+ax+2b=0的一个根在区间(0,1)内,另一个根在区间(1,2)内,
∴可得$\left\{\begin{array}{l}{b>0}\\{a+2b+1<0}\\{a+b+2>0}\end{array}\right.$.
作出满足上述不等式组对应的点(a,b)所在的平面区域,
得到△ABC及其内部,即如图所示的阴影部分(不含边界).
其中A(-3,1),B(-2,0),C(-1,0),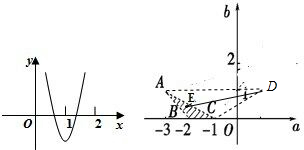
设点E(a,b)为区域内的任意一点,
则$\frac{b-a}{a-1}$=$\frac{b-1}{a-1}$-1,k=$\frac{b-1}{a-1}$,表示点E(a,b)与点D(1,1)连线的斜率
结合图形可知:0<k<$\frac{1}{2}$,
∴$\frac{b-a}{a-1}$的取值范围是(-1,-$\frac{1}{2}$).
故答案为:(-1,-$\frac{1}{2}$).
点评 本题给出含有参数a、b的一元二次方程满足的条件,求参数a、b满足的不等式组,并依此求关于a、b式子的取值范围.着重考查了二次函数的性质、零点存在性定理、二元一次不等式组表示的平面区域、直线的斜率公式与两点间的距离公式等知识,属于中档题.

 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案| A. | 0 | B. | $\sqrt{6}$ | C. | 6 | D. | 2$\sqrt{2}$ |
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\frac{5}{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 3 |
| A. | 平面ABCD∥平面ABB′A′ | B. | 平面ABCD∥平面ADD′A′ | ||
| C. | 平面ABCD∥平面CDD′C′ | D. | 平面ABCD∥平面A′B′C′D′ |
