题目内容
甲、乙两艘货轮都要在某个泊位停靠6小时,假定它们在一昼夜的时间段中随机到达,试求两船中有一艘在停泊位时,另一艘船必须等待的概率.
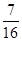
解析试题分析:因为甲、乙两船在一昼夜的时间中任何一个时间到达时等可能的,所以船在哪个时间到达的概率只与该时间段的长度有关,而与该时间段的位置无关,这符合几何概型的条件。设甲、乙两船到达泊位的时刻分别为x,y,试验的全部结果所构成的区域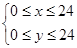 是一个正方形,若有一艘船必须等待,则
是一个正方形,若有一艘船必须等待,则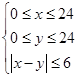 作出不等式组表示的平面区域,根据几何概型的求法,所求概率为两部分面积之比,
作出不等式组表示的平面区域,根据几何概型的求法,所求概率为两部分面积之比, .
.
试题解析:设甲、乙两船到达泊位的时刻分别为x,y.则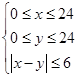 作出如图所示的区域.
作出如图所示的区域.
本题中,区域D的面积S1=242,
区域d的面积S2=242-182.∴P=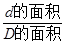 =
=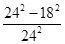 =
=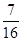 .
.
即两船中有一艘在停泊位时另一船必须等待的概率为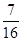 .
.
考点:几何概型的求法.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
为了调查学生的视力情况,随机抽查了一部分学生的视力,将调查结果分组,分组区间为 ,经过数据处理,得到如下频率分布表
,经过数据处理,得到如下频率分布表
| 分组 | 频数 | 频率 |
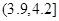 | 3 | 0.06 |
 | 6 | 0.12 |
 | 25 | 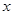 |
 | 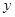 | 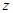 |
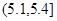 | 2 | 0.04 |
| 合计 | 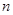 | 1.00 |
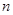 ,
,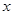 ,
,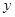 ,
,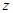 的值
的值(Ⅱ)从样本中视力在
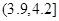 和
和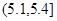 的所有同学中随机抽取两人,求两人视力差的绝对值低于
的所有同学中随机抽取两人,求两人视力差的绝对值低于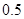 的概率
的概率 
 为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,
为随机变量,从棱长为1的正方体ABCD-A1B1C1D1的八个顶点中任取四个点,当四点共面时,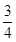 的社长是高中学生,
的社长是高中学生, 的社长是初中学生,高中社长中有
的社长是初中学生,高中社长中有 是高一学生,初中社长中有
是高一学生,初中社长中有 是初二学生.
是初二学生.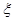 ,求
,求 .
.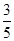 ,答对每道乙类题的概率都是
,答对每道乙类题的概率都是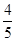 ,且各题答对与否相互独立.用
,且各题答对与否相互独立.用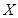 表示张同学答对题的个数,求
表示张同学答对题的个数,求
 名男生,
名男生, 名男生,
名男生, 人,请他们在班会上和全班同学分享学习心得.
人,请他们在班会上和全班同学分享学习心得.