题目内容
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月13日中的某一天到达该市,并停留2天.
(Ⅰ)求此人到达当日空气重度污染的概率;
(Ⅱ)设X是此人停留期间空气质量优良的天数,求X的分布列与数学期望.
(I)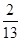 ;(II)分布列详见解析,期望为
;(II)分布列详见解析,期望为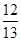 .
.
解析试题分析:(I) 3月1日至3月13日中,只有5日与8日为重度污染,再根据古典概率的求法即可得到所求概率;(Ⅱ)先确定X可能的取值0、1、2共三种,然后根据图像分别计算X为0、1及2时的概率.即可得到分布列,从而求出期望.
试题解析:设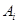 表示事件“此人于3月i日到达该市”(="1,2,,13)."
表示事件“此人于3月i日到达该市”(="1,2,,13)."
根据题意, 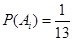 ,且
,且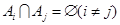 . 4分
. 4分
(I)设B为事件“此人到达当日空气重度污染”,则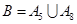 ,
,
所以 .
.
(II)由题意可知,X的所有可能取值为0,1,2,且
P(X=1)=P(A3∪A6∪A7∪A11)= P(A3)+P(A6)+P(A7)+P(A11)= 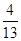 ,
,
P(X=2)=P(A1∪A2∪A12∪A13)= P(A1)+P(A2)+P(A12)+P(A13)= 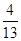 ,
,
P(X="0)=1-P(X=1)-P(X=2)=" 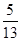 , 10分
, 10分
所以X的分布列为: 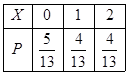 11分
11分
故X的期望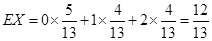 . 12分
. 12分
考点:1.古典概率;2.分布列与期望.

练习册系列答案
相关题目
在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为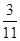 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | | |
| 乙班 | |  | |
| 合计 | | |  |
(2)根据列联表的数据,能否有
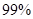 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的
 名学生从
名学生从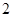 到
到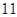 进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到
进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到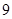 号或
号或 号的概率.
号的概率.  ,求
,求 .
. 、
、 、
、 。指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
。指标甲、乙、丙合格分别记为4分、2分、4分;若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。 就去打球;若
就去打球;若 就去唱歌;若
就去唱歌;若 就去下棋.
就去下棋.
 ,家长所得点数记为
,家长所得点数记为 ;
; ,家长的计算器产生的随机实数记为
,家长的计算器产生的随机实数记为 .
. ,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率; ,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率. .
.