题目内容
高三某班有两个数学课外兴趣小组,第一组有 名男生,
名男生, 名女生,第二组有
名女生,第二组有 名男生,
名男生, 名女生.现在班主任老师要从第一组选出
名女生.现在班主任老师要从第一组选出 人,从第二组选出
人,从第二组选出 人,请他们在班会上和全班同学分享学习心得.
人,请他们在班会上和全班同学分享学习心得.
(Ⅰ)求选出的 人均是男生的概率;
人均是男生的概率;
(Ⅱ)求选出的 人中有男生也有女生的概率.
人中有男生也有女生的概率.
(Ⅰ)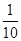 ;(Ⅱ)
;(Ⅱ)
解析试题分析:(Ⅰ)先列举出从第一组选出 人,从第二组选出
人,从第二组选出 人的所有基本事件共有30种,然后从中可数出选出的
人的所有基本事件共有30种,然后从中可数出选出的 人均是男生的共有3种,故可得
人均是男生的共有3种,故可得 ;(Ⅱ)由(Ⅰ)所列举的事件可知“选出的3个人有男生也有女生”的事件有25种,所以选出的3人中有男生也有女生的概率为
;(Ⅱ)由(Ⅰ)所列举的事件可知“选出的3个人有男生也有女生”的事件有25种,所以选出的3人中有男生也有女生的概率为 .
.
试题解析:(Ⅰ)记第一组的4人分别为 ;第二组的5人分别为
;第二组的5人分别为 1分
1分
设“从第一组选出 人,从第二组选出
人,从第二组选出 人”组成的基本事件空间为
人”组成的基本事件空间为 ,则
,则
 共有30种. 4分
共有30种. 4分
设“选出的 人均是男生”为事件
人均是男生”为事件 ,则事件A含有3个基本事件 6分
,则事件A含有3个基本事件 6分 ,所以选出的
,所以选出的 人均是男生的概率为
人均是男生的概率为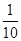 8分
8分
(Ⅱ)设“选出的3个人有男生也有女生”为事件B,则事件B含有25个基本事件, 10分 ,所以选出的
,所以选出的 人中有男生也有女生的概率为
人中有男生也有女生的概率为 . 13分
. 13分
考点:古典概率的求法

练习册系列答案
相关题目
某公司欲招聘员工,从1000名报名者中筛选200名参加笔试,按笔试成绩择优取50名面试,再从面试对象中聘用20名员工.
(Ⅰ)求每个报名者能被聘用的概率;
(Ⅱ)随机调查了24名笔试者的成绩如下表所示:
| 分数段 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) | [85,90) |
| 人数 | 1 | 2 | 6 | 9 | 5 | 1 |
(Ⅲ)公司从聘用的四男
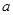 、
、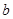 、
、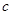 、
、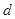 和二女
和二女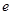 、
、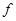 中选派两人参加某项培训,则选派结果为一男一女的概率是多少?
中选派两人参加某项培训,则选派结果为一男一女的概率是多少? 在一次联考后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于 分为优秀,
分为优秀, 分以下为非优秀,统计成绩后,得到如下的
分以下为非优秀,统计成绩后,得到如下的 列联表,且已知在甲、乙两个文科班全部
列联表,且已知在甲、乙两个文科班全部 人中随机抽取人为优秀的概率为
人中随机抽取人为优秀的概率为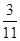 .
.
| | 优秀 | 非优秀 | 合计 |
| 甲班 |  | | |
| 乙班 | |  | |
| 合计 | | |  |
(2)根据列联表的数据,能否有
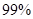 的把握认为成绩与班级有关系?
的把握认为成绩与班级有关系?(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的
 名学生从
名学生从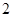 到
到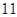 进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到
进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号,试求抽到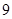 号或
号或 号的概率.
号的概率. 为了对某课题进行研究,用分层抽样方法从三所科研单位A、B、C的相关人员中,抽取若干人组成研究小组,有关数据见下表(单位:人):
| 科研单位 | 相关人数 | 抽取人数 |
| A | 16 | 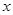 |
| B | 12 | 3 |
| C | 8 | 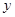 |
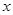 与
与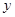 的值;
的值;(2)若从科研单位A、C抽取的人中选2人作专题发言,求这2人都来自科研单位A的概率.
 R
R ,若
,若 是从区间
是从区间 中随机抽取的一个数,
中随机抽取的一个数, 是从区间
是从区间 中随机抽取的一个数,求方程
中随机抽取的一个数,求方程 没有实数根的概率.
没有实数根的概率. 就去打球;若
就去打球;若 就去唱歌;若
就去唱歌;若 就去下棋.
就去下棋.
 ,家长所得点数记为
,家长所得点数记为 ;
; ,家长的计算器产生的随机实数记为
,家长的计算器产生的随机实数记为 .
. ,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率;
,则奖励宝宝一朵小红花,求抛掷一次后宝宝得到一朵小红花的概率; ,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率.
,则奖励宝宝一本兴趣读物,求按下一次按钮后宝宝得到一本兴趣读物的概率. 、
、 、
、 三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加
三组测试项目供参考人员选择,甲、乙、丙、丁、戊五人参加招聘,其中甲、乙两人各自独立参加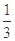 ,丙、丁两人各自通过测试的概率均为
,丙、丁两人各自通过测试的概率均为 .戊参加
.戊参加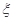 ,求
,求