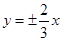题目内容
(本题满分12分)
在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在x轴上.
(1)求抛物线C的标准方程;
(2)设直线l是抛物线的准线,求证:以AB为直径的圆与准线l相切.
在平面直角坐标系xOy中,抛物线C的顶点在原点,经过点A(2,2),其焦点F在x轴上.
(1)求抛物线C的标准方程;
(2)设直线l是抛物线的准线,求证:以AB为直径的圆与准线l相切.
(1) y2=2x (2)关键证明AB的中点到准线的距离等于AB的一半。
试题分析:解:(1)设抛物线y2=2px(p>0),将点(2,2)代入得p=1.
∴y2=2x为所求抛物线的方程.
(2)证明:设lAB的方程为:x=ty+
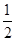 ,代入y2=2x得:y2-2ty-1=0,设AB的中点为M(x0,y0),则y0=t,x0=
,代入y2=2x得:y2-2ty-1=0,设AB的中点为M(x0,y0),则y0=t,x0=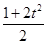 .
.∴点M到准线l的距离d=x0+
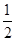 =
=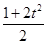 +
+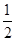 =1+t2.又AB=2x0+p=1+2t2+1=2+2t2,∴d=
=1+t2.又AB=2x0+p=1+2t2+1=2+2t2,∴d=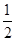 AB,故以AB为直径的圆与准线l相切.
AB,故以AB为直径的圆与准线l相切.点评:求抛物线的方程,前提是设抛物线的方程,而设置抛物线可结合焦点,像本题通过画图,知道抛物线的焦点在x轴的正半轴上,因而可令抛物线的方程为y2=2px(p>0)(式子中的x 对应x轴,2px前面是正的对应正半轴)。第二题涉及直线与抛物线这两种曲线,当两者相交时,常常在联立方程组后,用到根与系数的关系式:
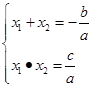

练习册系列答案
相关题目

 与
与 轴交于点
轴交于点 ,与直线
,与直线
 交于点
交于点 ,椭圆
,椭圆 以
以 为右焦点,且过点
为右焦点,且过点 时,椭圆
时,椭圆



 的一条渐近线方程为
的一条渐近线方程为 ,则其离心率为 。
,则其离心率为 。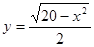 与直线L:
与直线L: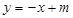 仅有一个公共点,求m的范围.
仅有一个公共点,求m的范围.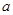 ,0)作椭圆
,0)作椭圆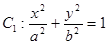 的弦,弦中点的轨迹仍是椭圆,记为
的弦,弦中点的轨迹仍是椭圆,记为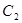 ,若
,若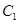 和
和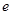 和
和 ,则
,则 的坐标分别是
的坐标分别是 ,直线
,直线 相交于点
相交于点 ,且直线
,且直线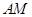 与直线
与直线 的斜率之差是
的斜率之差是 ,则点
,则点
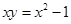


 为钝角,则此椭圆的离心率的取值范围为
为钝角,则此椭圆的离心率的取值范围为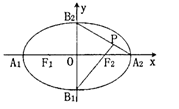
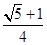 )
)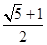 )
)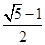 ,1)
,1) ,
, ,O为坐标原点,动点E满足:
,O为坐标原点,动点E满足:
 引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值.
引两条切线PA、PB,切点分别为A、B,直线AB与x轴、y轴分别交于M、N两点,求ΔMON面积的最小值. 的右焦点为
的右焦点为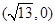 ,则该双曲线的渐近线方程为( )
,则该双曲线的渐近线方程为( )