题目内容
已知双曲线 的一条渐近线方程为
的一条渐近线方程为 ,则其离心率为 。
,则其离心率为 。
 的一条渐近线方程为
的一条渐近线方程为 ,则其离心率为 。
,则其离心率为 。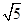
试题分析:根据题意可知,双曲线的焦点在x轴上,则可知其渐近线方程为
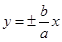 ,由于给定的渐近线斜率为2,则可知
,由于给定的渐近线斜率为2,则可知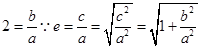 ,则可知e=
,则可知e=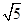 ,故答案为
,故答案为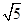 。
。点评:解决该试题的关键是理解双曲线的渐近线方程的表示得到参数a,b的比值,进而利用a,b,c的三者的关系得到a,c的比值,进而得到离心率,属于基础题。

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
题目内容
 的一条渐近线方程为
的一条渐近线方程为 ,则其离心率为 。
,则其离心率为 。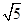
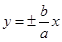 ,由于给定的渐近线斜率为2,则可知
,由于给定的渐近线斜率为2,则可知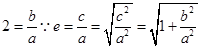 ,则可知e=
,则可知e=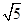 ,故答案为
,故答案为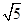 。
。
 导学全程练创优训练系列答案
导学全程练创优训练系列答案