题目内容
4.求12+22+32+…+n2<1000成立的n的最大整数值,写出程序语句,并画出框图.分析 这是一个累加求和问题,可设计一个计数变量,一个累加变量,用循环结构实现这一算法.
解答 解:程序如下:
S=0
n=1
While S<1000
S=S+n2
n=n+1
End while
Print n-2
框图如下: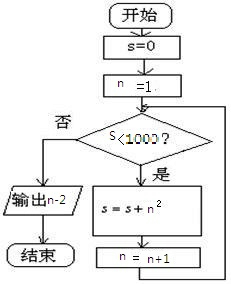
点评 本题主要考查设计程序框图解决实际问题.在一些算法中,也经常会出现从某处开始,按照一定条件,反复执行某一处理步骤的情况,这就是循环结构.循环结构要在某个条件下终止循环,这就需要条件分支结构来判断.在循环结构中都有一个计数变量和累加变量.计数变量用于记录循环次数,累加变量用于输出结果,计数变量和累加变量一般是同步执行的,累加一次,计数一次.

练习册系列答案
相关题目
2.函数y=ln(2x+5)的导函数f′(x)=( )
| A. | $\frac{1}{2x+5}$ | B. | $\frac{2}{2x+5}$ | C. | $\frac{5}{2x+5}$ | D. | $\frac{ln2}{2x+5}$ |
9.若一个命题的结论是“直线l在平面α内”,则用反证法证明这个命题时,第一步应作的假设为( )
| A. | 假设直线l∥平面α | B. | 假设直线l∩平面α于点A | ||
| C. | 假设直线l?平面α | D. | 假设直线l⊥平面α |
16.曲线y=ax3-2bx+1在点(1,f(1))处的切线方程为y=-x+2,则a+2b=( )
| A. | -1 | B. | 1 | C. | 2 | D. | 3 |
14.使平面α∥平面β的一个条件是( )
| A. | 存在一条直线a,a∥α,a∥β | |
| B. | 存在一条直线a,a?α,a∥β | |
| C. | 存在两条平行直线a、b,a?α,b?β,a∥β,b∥α | |
| D. | 存在两条异面直线a、b,a?α,b?β,a∥β,b∥α |