题目内容
已知函数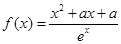 ,其
,其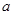 中为常数,
中为常数,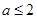 .
.
(1)当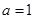 时,求曲线
时,求曲线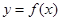 在点
在点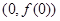 处的切线方程;
处的切线方程;
(2)是否存在实数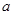 ,使
,使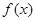 的极大值为
的极大值为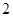 ?若存在,求出
?若存在,求出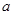 的值;若不存在,说明理由.
的值;若不存在,说明理由.
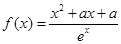 ,其
,其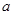 中为常数,
中为常数,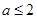 .
.(1)当
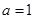 时,求曲线
时,求曲线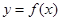 在点
在点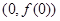 处的切线方程;
处的切线方程;(2)是否存在实数
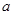 ,使
,使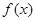 的极大值为
的极大值为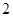 ?若存在,求出
?若存在,求出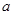 的值;若不存在,说明理由.
的值;若不存在,说明理由.(1)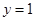 ;(2)不存在.
;(2)不存在.
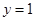 ;(2)不存在.
;(2)不存在.试题分析:(1)由题意
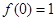 ,而曲线在点
,而曲线在点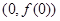 处的切线的斜率为
处的切线的斜率为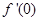 ,因此先求导数,
,因此先求导数,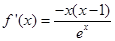 ,得
,得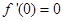 ,故切线方程为
,故切线方程为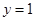 ;(2)这种存在性命题都是先假设存在,然后去求参数
;(2)这种存在性命题都是先假设存在,然后去求参数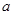 的值,如能求得,则存在,如求不出,说明假设错误,结论就是不存在,利用导数公式可得
的值,如能求得,则存在,如求不出,说明假设错误,结论就是不存在,利用导数公式可得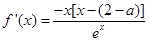 ,极值点是使
,极值点是使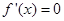 的点,本题中可得
的点,本题中可得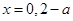 ,由于已知条件是
,由于已知条件是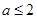 ,可分类讨论,
,可分类讨论,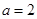 时,
时,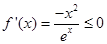 在
在 上恒成立,即
上恒成立,即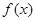 在
在 上单调递减,无极值,当
上单调递减,无极值,当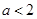 时,
时,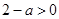 ,通过讨论
,通过讨论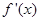 在
在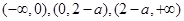 上的符号,确定出
上的符号,确定出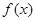 的单调性,也即确定出极大值点有
的单调性,也即确定出极大值点有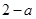 ,极大值为
,极大值为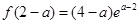 ,接下来考虑的是
,接下来考虑的是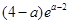 能否等于2,解方程
能否等于2,解方程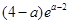
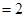 是不可能的(可以猜测计算出
是不可能的(可以猜测计算出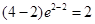 ),可讨论函数
),可讨论函数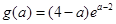 的单调性,确定其值域或最值。
的单调性,确定其值域或最值。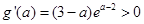 ,因此
,因此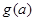 在
在 单调递增,从而
单调递增,从而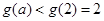 ,故
,故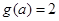 无解,
无解,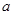 不存在.
不存在.试题解析:(1)
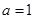 ,
,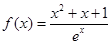 ,
,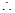
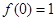 , 1分
, 1分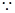
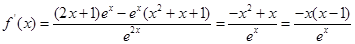 ,
,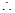
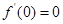 3分
3分则曲线在
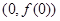 处的切线方程为
处的切线方程为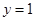 . 5分
. 5分(2)
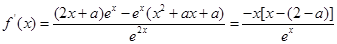
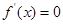 的根为
的根为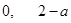 , 6分
, 6分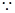
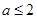 ,
,

当
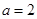 时,
时,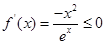 ,
,
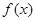 在
在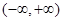 递减,无极值; 8分
递减,无极值; 8分当
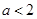 时,
时,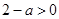 ,
,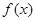 在
在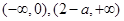 递减,在
递减,在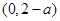 递增;
递增;
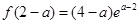 为
为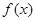 的极大值, 10分
的极大值, 10分令
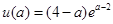 ,
,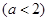 ,
,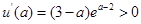
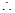
 在
在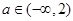 上递增,
上递增,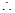
 ,
,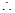 不存在实数
不存在实数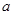 ,使
,使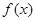 的极大值为
的极大值为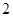 . 13分
. 13分
练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
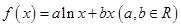 在点
在点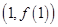 处的切线方程为
处的切线方程为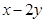
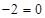 .
.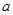 、
、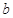 的值;
的值; 时,
时,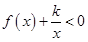 恒成立,求实数
恒成立,求实数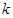 的取值范围;
的取值范围;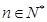 ,且
,且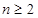 时,
时,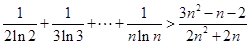 .
.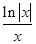 ,则函数y=f(x)的大致图象为( )
,则函数y=f(x)的大致图象为( )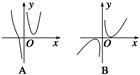
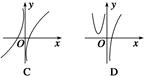
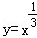
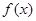 是定义在
是定义在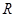 上的奇函数,对任意
上的奇函数,对任意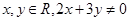 ,都有
,都有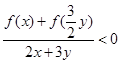 ,若
,若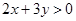 ,则( )
,则( )
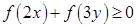
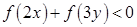
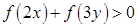
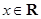 ,
,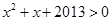 ”的否定是“任意
”的否定是“任意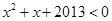 ”
” 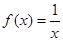 在其定义域上是减函数
在其定义域上是减函数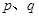 ,若“
,若“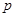 且
且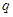 ”是真命题,则
”是真命题,则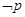 是假命题
是假命题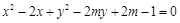 ,当圆的面积最小时,直线
,当圆的面积最小时,直线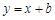 与圆相切,则
与圆相切,则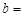 .
. 函数
函数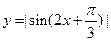 的最小正周期是
的最小正周期是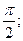
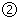 函数
函数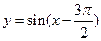 在区间
在区间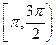 上单调递增;
上单调递增;
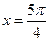 是函数
是函数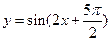 的图象的一条对称轴。其中正确命题的个数是( )
的图象的一条对称轴。其中正确命题的个数是( )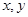 为实数,且满足:
为实数,且满足: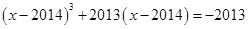 ,
,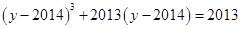 ,则
,则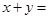 .
.