题目内容
(本小题满分14分)已知函数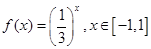 ,函数
,函数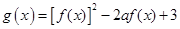 的最小值为
的最小值为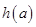 ,
,
(1)当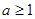 时,求
时,求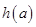
(2)是否存在实数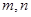 同时满足下列条件:①
同时满足下列条件:①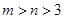 ;②当
;②当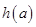 的定义域为
的定义域为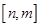 时,值域为
时,值域为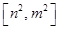
 ?若存在,求出
?若存在,求出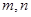 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。
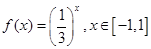 ,函数
,函数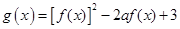 的最小值为
的最小值为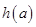 ,
,(1)当
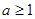 时,求
时,求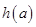
(2)是否存在实数
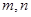 同时满足下列条件:①
同时满足下列条件:①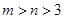 ;②当
;②当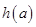 的定义域为
的定义域为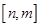 时,值域为
时,值域为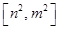
 ?若存在,求出
?若存在,求出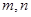 的值;若不存在,请说明理由。
的值;若不存在,请说明理由。(1)当 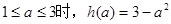 ,当
,当 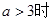 ,
,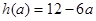 ;
;
(2) 。
。
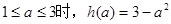 ,当
,当 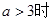 ,
,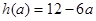 ;
;(2)
 。
。试题分析:(1)g(x)为关于f(x)的二次函数,可用换元法,转化为二次函数在特定区间上的最值问题,定区间动轴;
(2)由(1)可知a≥3时,h(a)为一次函数且为减函数,求值域,找关系即可.
(1)
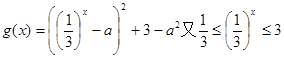
当
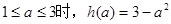
当
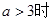 ,
,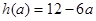 。。。。。。。7分
。。。。。。。7分(2)假设满足题意的
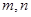 存在,
存在,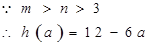 在
在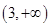 上是减函数。
上是减函数。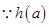 的定义域为
的定义域为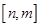 ,值域为
,值域为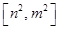 ,
,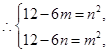 得
得 ,
,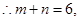 但这与
但这与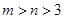 矛盾。
矛盾。 。。。。。14分
。。。。。14分点评:解决该试题的关键是理解二次函数在特定区间上的值域问题一般结合图象和单调性处理,“定轴动区间”、“定区间动轴”.

练习册系列答案
相关题目
 .
.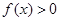 的解集为
的解集为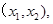 且方程
且方程 的两实根为
的两实根为 .
. ,求
,求 的关系式;
的关系式;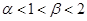 ,求证:
,求证: .
.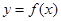 在点
在点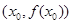 处的切线方程为
处的切线方程为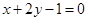 ,则
,则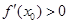
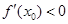
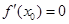
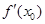 不存在
不存在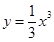 上的点
上的点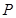 的切线
的切线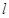 的方程为
的方程为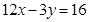 ,那么
,那么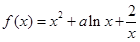 在
在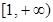 上是单调递增函数,求实数
上是单调递增函数,求实数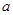 的取值范围.
的取值范围.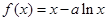 ,
,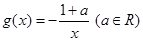 .
.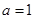 ,求函数
,求函数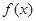 的极值;
的极值;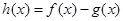 ,求函数
,求函数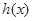 的单调区间;
的单调区间; 上不存在
上不存在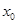 ,使得
,使得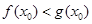 成立,求实数
成立,求实数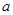 的取值范围.
的取值范围.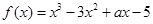 在
在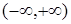 上单调递增,则
上单调递增,则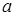 的取值范围是 .
的取值范围是 .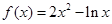 在其定义域的一个子区间
在其定义域的一个子区间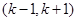 内部是单调函数,则实数
内部是单调函数,则实数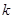 的取值范围是 ( )
的取值范围是 ( )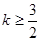
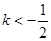
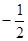 <
<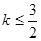
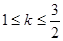
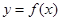 的图象在点
的图象在点 处的切线方程是
处的切线方程是 ,则
,则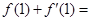 _.
_.