题目内容
19.化简(1)$\sqrt{1-si{n}^{2}440°}$
(2)$\frac{\sqrt{1-2sin10°cos10°}}{sin10°-\sqrt{1-si{n}^{2}10°}}$.
分析 (1)利用平方关系把根式内部的代数式转化为余弦,开方后得答案;
(2)把分式分子化为完全平方式的形式,然后开方,分母利用平方关系化为余弦开方,则答案可求.
解答 解:(1)$\sqrt{1-si{n}^{2}440°}$=$\sqrt{co{s}^{2}440°}$=|cos440°|=|cos(360°+80°)|=cos80°;
(2)$\frac{\sqrt{1-2sin10°cos10°}}{sin10°-\sqrt{1-si{n}^{2}10°}}$=$\frac{\sqrt{(sin10°-cos10°)^{2}}}{sin10°-\sqrt{co{s}^{2}10°}}$
=$\frac{cos10°-sin10°}{sin10°-cos10°}=-1$.
点评 本题考查三角函数的化简求值,训练了同角三角函数基本关系的应用,是基础题.

练习册系列答案
相关题目
11.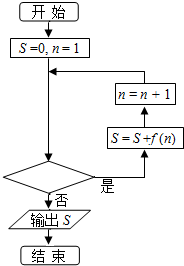 已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
 已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )
已知函数$f(x)=\frac{1}{{\sqrt{x}+\sqrt{x-1}}}$,程序框图如图所示,若输出的结果S=10,则判断框中可以填入的关于n的判断条件是( )| A. | n≤100? | B. | n≤99? | C. | n>100? | D. | n>99? |