题目内容
10.圆周上有4个点,以其中的3个顶点画三角形,一共可以画出不同三角形的个数是( )| A. | C${\;}_{4}^{3}$ | B. | A${\;}_{4}^{3}$ | C. | 43 | D. | 34 |
分析 根据题意,圆周上任意三点不共线,则圆周上任意取三点都可以做出一个三角形,由组合式直接计算可得答案.
解答 解:根据题意,圆周上任意三点不共线,则圆周上任意取三点都可以做出一个三角形,
则圆周上有4个点,以其中的3个顶点画三角形,在4个点中任取3个点即可,
一共可以画出C43个三角形,
故选:A.
点评 本题考查组合数公式的运用,注意“圆周上任意三点不共线”的性质.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
18.过定点(1,2)可作两条直线与圆x2+y2+2kx+2y=k2+1相切,则实数k的取值范围为( )
| A. | (-∞,-2)∪(4,+∞) | B. | (-2,4) | C. | (-∞,4) | D. | (-2,+∞) |
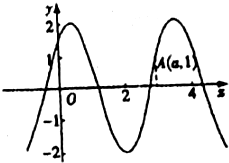 已知函数f(x)=2sin(2x+$\frac{π}{4}$)的部分图象如图所示.
已知函数f(x)=2sin(2x+$\frac{π}{4}$)的部分图象如图所示.