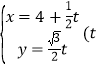题目内容
【题目】已知函数![]() ,点
,点![]() 为一定点,直线
为一定点,直线![]() 分别与函数
分别与函数![]() 的图象和
的图象和![]() 轴交于点
轴交于点![]() ,
,![]() ,记
,记![]() 的面积为
的面积为![]() .
.
(Ⅰ)当![]() 时,求函数
时,求函数![]() 的单调区间;
的单调区间;
(Ⅱ)当![]() 时,若
时,若![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(Ⅰ)![]() 在
在![]() ,
,![]() 上单调递增,在
上单调递增,在![]() 上单调递减;(Ⅱ)
上单调递减;(Ⅱ) ![]()
【解析】
(Ⅰ)由已知可得:![]() ,分别对
,分别对![]() 和
和![]() 时的
时的![]() 进行求导分析即可;
进行求导分析即可;
(Ⅱ)当![]() ,
,![]() 时,
时,![]() ,由已知可得当
,由已知可得当![]() 时,
时,![]() ,求导,得:
,求导,得:![]() ,由此可得当
,由此可得当![]() 时,
时,![]() ,当
,当![]() ,
,![]() ,问题得解.
,问题得解.
(Ⅰ)由已知可得:当![]() 时,
时,
![]()
当![]() 时,
时,![]() ,则
,则![]()
显然此时![]() ,所以
,所以![]() 在
在![]() 上单调递增;
上单调递增;
当![]() 时,
时,![]() ,则
,则![]()
当![]() 时,
时,![]() ;
;![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(Ⅱ)当![]() ,
,![]() 时,
时,![]()
因为![]() ,使得
,使得![]() ,所以当
,所以当![]() 时,
时,![]() .
.
求导,得:![]()
由![]() 可得
可得![]() ,
,
①当![]() ,即
,即![]() 时,
时,![]() 对
对![]() 成立,
成立,
所以![]() 在
在![]() 上单调递增,故
上单调递增,故![]()
由![]() ,解得
,解得![]()
所以![]() 满足题意;
满足题意;
②当![]() ,即
,即![]() 时,
时,
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,
,
所以![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]()
由![]() ,解得
,解得![]() ,
,
所以![]() 满足题意.
满足题意.
综上所述:实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
【题目】2019年10月18日-27日,第七届世界军人运动会在湖北武汉举办,中国代表团共获得133金64银42铜,共239枚奖牌.为了调查各国参赛人员对主办方的满意程度,研究人员随机抽取了500名参赛运动员进行调查,所得数据如下所示,现有如下说法:①在参与调查的500名运动员中任取1人,抽到对主办方表示满意的男性运动员的概率为![]() ;②在犯错误的概率不超过1%的前提下可以认为“是否对主办方表示满意与运动员的性别有关”;③没有99.9%的把握认为“是否对主办方表示满意与运动员的性别有关”;则正确命题的个数为( )附:
;②在犯错误的概率不超过1%的前提下可以认为“是否对主办方表示满意与运动员的性别有关”;③没有99.9%的把握认为“是否对主办方表示满意与运动员的性别有关”;则正确命题的个数为( )附:
男性运动员 | 女性运动员 | |||||
对主办方表示满意 | 200 | 220 | ||||
对主办方表示不满意 | 50 | 30 | ||||
| 0.100 | 0.050 | 0.010 | 0.001 | ||
k | 2.706 | 3.841 | 6.635 | 10.828 | ||
A.0B.1C.2D.3