题目内容
(本小题满分12分)
已知双曲 线的渐近线方程为y=±x,并且焦点都在圆x2+y2=100上,求双曲线方程.
线的渐近线方程为y=±x,并且焦点都在圆x2+y2=100上,求双曲线方程.
已知双曲
 线的渐近线方程为y=±x,并且焦点都在圆x2+y2=100上,求双曲线方程.
线的渐近线方程为y=±x,并且焦点都在圆x2+y2=100上,求双曲线方程.所求双曲线方程为-=1或-=1
解:(1)当焦点在x轴上时,设双曲线方程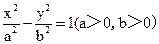
由渐近线方程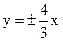 得
得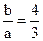 ,①
,①
又焦点在圆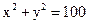 上,知c=10,
上,知c=10,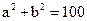 ②
②
由①②解得a=6,b=8
∴所求双曲线方程为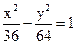
(2)当焦点在y轴上时,设双 曲线方程为-=1(a>0,b>0),
曲线方程为-=1(a>0,b>0),
则⇒
∴所求双曲线方程为-=1.
综上,所求双曲线方程为-=1或-=1.
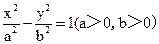
由渐近线方程
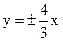 得
得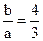 ,①
,①又焦点在圆
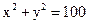 上,知c=10,
上,知c=10,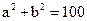 ②
②由①②解得a=6,b=8
∴所求双曲线方程为
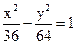
(2)当焦点在y轴上时,设双
 曲线方程为-=1(a>0,b>0),
曲线方程为-=1(a>0,b>0),则⇒
∴所求双曲线方程为-=1.
综上,所求双曲线方程为-=1或-=1.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
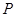 为双曲线
为双曲线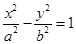
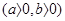 的右支上一点,
的右支上一点,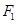 、
、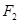 为双曲线的左、右焦点,使
为双曲线的左、右焦点,使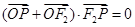 (
(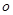 为坐标原点),且
为坐标原点),且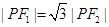 ,则双曲线离率为( )
,则双曲线离率为( )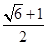
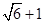
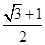
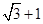
 分)已知双曲线
分)已知双曲线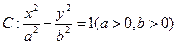 的离心率为
的离心率为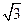 ,且双曲线上点到右焦点的距离与到直线
,且双曲线上点到右焦点的距离与到直线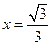 的距离之比为
的距离之比为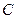 的方程;
的方程;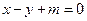 与双曲线
与双曲线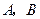 ,且线段
,且线段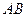 的中点在圆
的中点在圆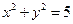 上,求
上,求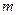 的值.
的值. 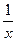 上任意一点P处的切线与两坐标轴围成的三角形面积
上任意一点P处的切线与两坐标轴围成的三角形面积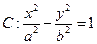 ,F为右焦点,过F作双曲线C在第一、三象限的渐近线的垂线
,F为右焦点,过F作双曲线C在第一、三象限的渐近线的垂线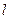 ,若
,若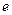 的取值范围为
的取值范围为 ),虚轴长为
),虚轴长为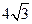 ,则双曲线的方程为( ).
,则双曲线的方程为( ).
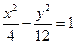

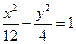
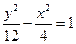
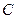 与双曲线
与双曲线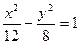 共渐近线,且过点
共渐近线,且过点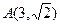 ,则双曲线
,则双曲线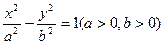 的两焦点,以线段F1F2为边作正三角形,若双曲线恰好平分正三角形的另两边,则双曲线的离心率是 ( )
的两焦点,以线段F1F2为边作正三角形,若双曲线恰好平分正三角形的另两边,则双曲线的离心率是 ( )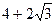
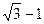
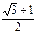
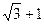
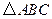 是等腰三角形,
是等腰三角形,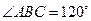 ,则以
,则以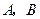 为焦点且过点
为焦点且过点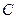 的双曲线的离心率为
的双曲线的离心率为