题目内容
19.一名刚参加工作的大学生为自己定制的每月用餐费的低标准是240元,又知其他费用最少需支出180元,而每月可用来支配的资金为500元,这名新员工可以如何使用这些钱?请用不等式(组)表示出来,并画出对应的平面区域.分析 设用餐费为x元,其他费用为y元,根据条件建立不等式关系即可得到结论.
解答 解:设用餐费为x元,其他费用为y元,由题意知x不小于240,y不小于180,x与y的和不超过500,用不等式组表示为$\left\{\begin{array}{l}{x+y≤500}\\{x≥240}\\{y≥180}\end{array}\right.$,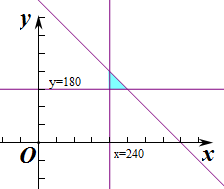
对应的平面区域如图阴影部分所示.
点评 本题主要考查二元一次不等式组表示平面区域,根据条件建立不等式关系是解决本题的关键.

练习册系列答案
相关题目
7.在△ABC中,AB=2BC,以A,B为焦点,经过C的椭圆和双曲线的离心率分别为e1,e2,则( )
| A. | $\frac{1}{{e}_{1}}$-$\frac{1}{{e}_{2}}$=1 | B. | $\frac{1}{{e}_{1}}$-$\frac{1}{{e}_{2}}$=2 | C. | $\frac{1}{{{e}_{1}}^{2}}$-$\frac{1}{{{e}_{2}}^{2}}$=1 | D. | $\frac{1}{{{e}_{1}}^{2}}$-$\frac{1}{{{e}_{2}}^{2}}$=2 |
8.双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a、b>0)的左、右焦点分别为F1、F2,过F2作一条直线与两条渐近线分别交于P、Q两点,线段QF2的垂直平分线恰好为双曲线C的一条渐近线,则双曲线C的离心率为( )
| A. | $\sqrt{3}$ | B. | 2 | C. | $\frac{\sqrt{6}}{2}$ | D. | $\frac{2\sqrt{3}}{3}$ |