题目内容
14．已知直线l过两点A（3，2），B（8，12）且点C（-2，a）在直线上，则a=-8．分析 直线l过两点A（3，2），B（8，12）且点C（-2，a）在直线上，可得kAB=kAC，利用斜率计算公式即可得出．
解答 解：∵直线l过两点A（3，2），B（8，12）且点C（-2，a）在直线上，
∴kAB=kAC，
∴$\frac{12-2}{8-3}$=$\frac{a-2}{-2-3}$，
解得a=-8．
故答案为：-8．
点评 本题考查了三点共线与斜率的关系、斜率计算公式，考查了计算能力，属于基础题．
练习册系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的右焦点为F，椭圆过（2，$\sqrt{2}$）且离心率为$\frac{{\sqrt{2}}}{2}$，
2．已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1（a＞b＞0）$的左焦点为F，右顶点为A，点P在椭圆上，直线AP交y轴于点M，若$\overrightarrow{PF}$=$\sqrt{3}\overrightarrow{MO}$（O为坐标原点），则椭圆的离心率是（ ）
| A． | $\frac{\sqrt{2}}{2}$ | B． | $\sqrt{3}-1$ | C． | $\frac{\sqrt{3}}{2}$ | D． | $\frac{1}{3}$ |
3．设x，y满足约束条件$\left\{\begin{array}{l}{x-2y≥-2}\\{3x-2y≤3}\\{x+y≥1}\end{array}\right.$，若x2+4y2≥m恒成立，则实数m的最大值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{3}{4}$ | C． | $\frac{4}{5}$ | D． | $\frac{5}{6}$ |
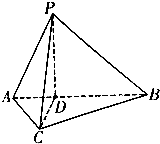如图所示，三棱锥P-ABC中，点D为线段AB上一点，AC⊥BC，PD⊥平面ABC，AD=$\frac{1}{2}$DB，PD=BD，∠ABC=30°．