题目内容
已知函数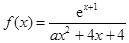 ,其中
,其中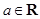 .
.
(1)若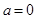 ,求函数
,求函数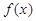 的极值;
的极值;
(2)当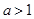 时,试确定函数
时,试确定函数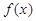 的单调区间.
的单调区间.
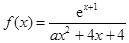 ,其中
,其中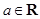 .
.(1)若
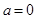 ,求函数
,求函数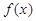 的极值;
的极值;(2)当
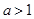 时,试确定函数
时,试确定函数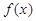 的单调区间.
的单调区间.(1)当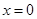 时,函数
时,函数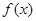 有极小值
有极小值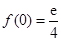 ;(2)当
;(2)当 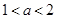 时,
时,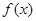 的单调减区间为
的单调减区间为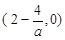 ,单调增区间为
,单调增区间为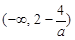 ,
,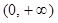 ;当
;当 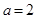 时,函数
时,函数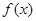 在
在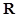 单调递增;当
单调递增;当 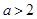 时,函数
时,函数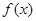 的单调减区间为
的单调减区间为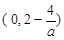 ;单调增区间为
;单调增区间为 ,
,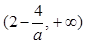 .
.
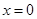 时,函数
时,函数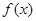 有极小值
有极小值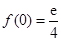 ;(2)当
;(2)当 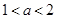 时,
时,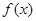 的单调减区间为
的单调减区间为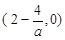 ,单调增区间为
,单调增区间为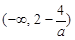 ,
,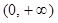 ;当
;当 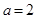 时,函数
时,函数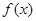 在
在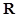 单调递增;当
单调递增;当 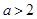 时,函数
时,函数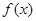 的单调减区间为
的单调减区间为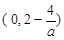 ;单调增区间为
;单调增区间为 ,
,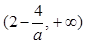 .
.试题分析:(1)若
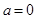 ,求函数
,求函数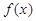 的极值,把
的极值,把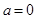 代入得函数
代入得函数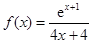 ,求它的极值,首先求定义域,对函数求导,求出导数等于零点,及两边导数的符号,从而确定极值点;(2)当
,求它的极值,首先求定义域,对函数求导,求出导数等于零点,及两边导数的符号,从而确定极值点;(2)当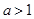 时,试确定函数
时,试确定函数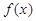 的单调区间,由于含有指数函数,可通过求导数来确定函数
的单调区间,由于含有指数函数,可通过求导数来确定函数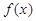 单调区间,因此先确定函数的定义域为
单调区间,因此先确定函数的定义域为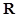 ,对函数
,对函数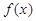 求导,令
求导,令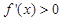 ,解不等式即可,但由于含有参数,需对参数讨论,分
,解不等式即可,但由于含有参数,需对参数讨论,分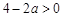 ,
,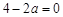 ,
,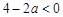 三种情况讨论,从而确定出单调区间.
三种情况讨论,从而确定出单调区间.(1)函数
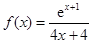 的定义域为
的定义域为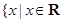 ,且
,且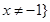 . 1分
. 1分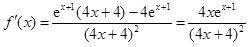 . 3分
. 3分令
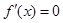 ,得
,得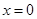 ,当
,当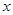 变化时,
变化时,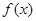 和
和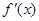 的变化情况如下:
的变化情况如下: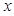 | 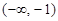 | 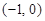 | 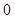 | 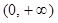 |
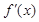 | 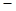 | 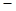 |  | 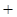 |
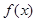 | ↘ | ↘ | | ↗ |
故
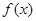 的单调减区间为
的单调减区间为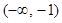 ,
,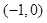 ;单调增区间为
;单调增区间为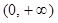 .
.所以当
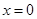 时,函数
时,函数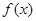 有极小值
有极小值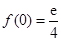 . 6分
. 6分(2)因为
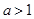 ,所以
,所以 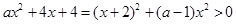 ,
,所以函数
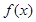 的定义域为
的定义域为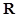 , 7分
, 7分求导,得
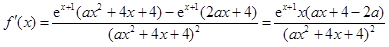 , 8分
, 8分令
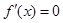 ,得
,得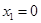 ,
,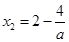 , 9分
, 9分当
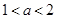 时,
时,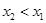 ,
,当
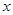 变化时,
变化时,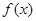 和
和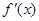 的变化情况如下:
的变化情况如下: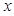 | 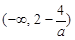 | 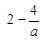 | 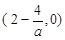 | 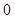 | 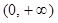 |
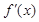 | 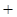 |  | 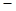 |  | 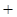 |
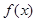 | ↗ | | ↘ | | ↗ |
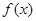 的单调减区间为
的单调减区间为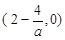 ,单调增区间为
,单调增区间为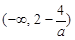 ,
,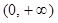 . 11分
. 11分当
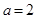 时,
时,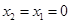 ,
,因为
 ,(当且仅当
,(当且仅当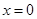 时,
时,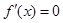 )
)所以函数
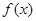 在
在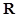 单调递增. 12分
单调递增. 12分当
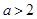 时,
时,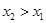 ,
,当
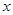 变化时,
变化时,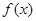 和
和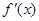 的变化情况如下:
的变化情况如下: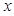 |  | 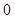 | 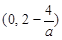 | 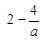 | 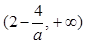 |
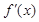 | 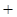 |  | 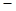 |  | 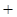 |
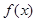 | ↗ | | ↘ | | ↗ |
故函数
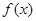 的单调减区间为
的单调减区间为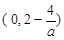 ,单调增区间为
,单调增区间为 ,
,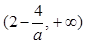 .
.综上,当
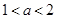 时,
时,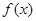 的单调减区间为
的单调减区间为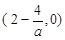 ,单调增区间为
,单调增区间为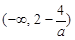 ,
,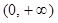 ;当
;当 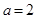 时,函数
时,函数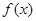 在
在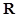 单调递增;当
单调递增;当 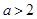 时,函数
时,函数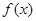 的单调减区间为
的单调减区间为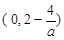 ;单调增区间为
;单调增区间为 ,
,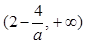 . 13分
. 13分
练习册系列答案
 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
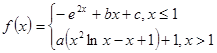 函数
函数 在
在 处取得极值1.
处取得极值1.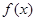 在区间[-2,2]上的最大值.
在区间[-2,2]上的最大值.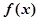 的导函数为
的导函数为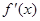 ,函数
,函数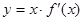 的图象的一部分如下图所示,则( )
的图象的一部分如下图所示,则( )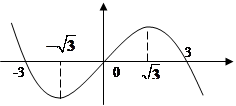
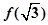 ,极小值为
,极小值为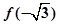
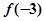 ,极小值为
,极小值为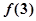
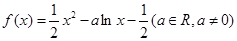 .
.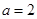 时,求曲线
时,求曲线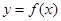 在点
在点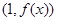 处的切线方程;
处的切线方程;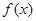 的单调区间;
的单调区间;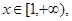 都有
都有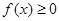 恒成立,求实数
恒成立,求实数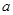 的取值范围.
的取值范围. 上的函数
上的函数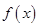 ,其导函数是
,其导函数是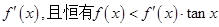 成立,则
成立,则


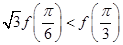
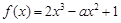 在区间
在区间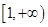 上为单调增函数,求
上为单调增函数,求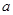 的取值范围.
的取值范围.