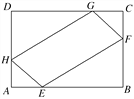
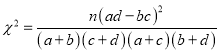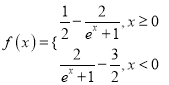题目内容
【题目】已知定义域为![]() 的单调递减的奇函数
的单调递减的奇函数![]() ,当
,当![]() 时,
时, ![]() .
.
(1)求![]() 的值;
的值;
(2)求![]() 的解析式;
的解析式;
(3)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)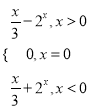 ;(3)
;(3)![]() .
.
【解析】试题分析:(1)根据函数为奇函数得![]() ,结合当
,结合当![]() 时,
时, ![]() ,即可求出
,即可求出![]() 的值;(2)由定义域为
的值;(2)由定义域为![]() 的函数
的函数![]() 是奇函数,知
是奇函数,知![]() .当
.当![]() 时,
时, ![]() ,由函数
,由函数![]() 是奇函数,知
是奇函数,知![]() ,由此能求出
,由此能求出![]() 的解析式;(3)由
的解析式;(3)由![]() 是
是![]() 上单调递减的奇函数,
上单调递减的奇函数, ![]() ,得
,得![]() 即
即![]() 恒成立,再由根的判别式小于零即可求出实数
恒成立,再由根的判别式小于零即可求出实数![]() 的取值范围.
的取值范围.
试题解析:(1)f(﹣1)=﹣f(1)=﹣(![]() ﹣2)=
﹣2)=![]() ;
;
(2)∵定义域为R的函数f(x)是奇函数,
∴f(0)=0,
当x<0时,﹣x>0,
f(﹣x)=﹣![]() ﹣2﹣x ,
﹣2﹣x ,
又∵函数f(x)是奇函数,
∴f(﹣x)=﹣f(x),
∴f(x)=![]() +2﹣x ,
+2﹣x ,
综上所述f(x)=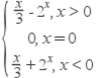 .
.
(3)∵f(1)=﹣![]() <f(0)=0,
<f(0)=0,
且f(x)在R上单调,
∴f(x)在R上单调递减,
由f(t2﹣2t)+f(2t2﹣k)<0,
得f(t2﹣2t)<﹣f(2t2﹣k),
∵f(x)是奇函数,
∴f(t2﹣2t)<f(k﹣2t2),
又∵f(x)是减函数,
∴t2﹣2t>k﹣2t2
即3t2﹣2t﹣k>0对任意t∈R恒成立,
∴△=4+12k<0得k<﹣![]() ,即为所求.
,即为所求.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目