题目内容
【题目】以 A 为圆心, 以![]() 为半径的圆外有一点 B , 已知
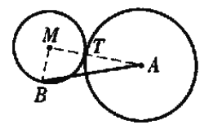
为半径的圆外有一点 B , 已知 ![]() =2sinθ.设过点B且与⊙A 外切于点T的圆的圆心为 M.
=2sinθ.设过点B且与⊙A 外切于点T的圆的圆心为 M.
(1)当 θ取某个值时, 说明点 M 的轨迹P 是什么曲线;
(2)点M 是轨迹 P上的动点, 点N 是 ⊙A上的动点, 把![]() 的最小值记为
的最小值记为![]() (不要求证明), 求
(不要求证明), 求![]() 的取值范围;
的取值范围;
(3)若将题设条件中的θ的范围改为![]() ,点 B 的位置改为⊙A内 , 其它条件不变,点 M的轨迹记为 P .试提出一个和(2)具有相同结构的有意义的问题(不要求解答).
,点 B 的位置改为⊙A内 , 其它条件不变,点 M的轨迹记为 P .试提出一个和(2)具有相同结构的有意义的问题(不要求解答).
【答案】(1) 点 M 的轨迹是以A、B 为焦点, 实轴长为2cos θ的双曲线的 靠近焦点B 的一支.(2) ![]() (3)见解析
(3)见解析
【解析】
(1)如图,连 MT 、MA 、MB , 显然 M 、T 、A 三点共线, 且![]() .
.
又![]() ,故
,故![]() ,其中
,其中![]()
故点 M 的轨迹是以A、B 为焦点, 实轴长为2cos θ的双曲线的 靠近焦点B 的一支.
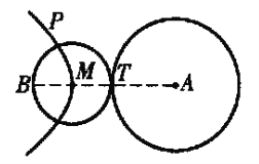
(2)显然, ![]() 的最小值
的最小值![]() 即为如图 所示的
即为如图 所示的 ![]() (N 和 T 重合).
(N 和 T 重合).
![]() .
.
故![]() .
.
由![]() ,知
,知![]() ,由此得
,由此得![]() .
.
(3)设点 M是轨迹P上的动点, 点N是⊙A上的动点, 把 ![]() 的最大值记为
的最大值记为![]() .求
.求![]() 的取值范围.
的取值范围.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】随着互联网的不断发展,手机打车软件APP也不断推出.在某地有AB两款打车APP,为了调查这两款软件叫车后等候的时间,用这两款APP分别随机叫了50辆车,记录了候车时间如下表:
A款软件:
候车时间(分钟) |
|
|
|
|
|
|
车辆数 | 2 | 12 | 8 | 12 | 14 | 2 |
B款软件:
候车时间(分钟) |
|
|
|
|
|
|
车辆数 | 2 | 10 | 28 | 7 | 2 | 1 |
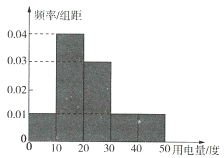
(1)试画出A款软件候车时间的频率分布直方图,并估计它的众数及中位数;
(2)根据题中所给的数据,将频率视为概率
(i)能否认为B款软件打车的候车时间不超过6分钟的概率达到了75%以上?
(ii)仅从两款软件的平均候车时间来看,你会选择哪款打车软件?