题目内容
【题目】在直角坐标系 ![]() 中,以原点
中,以原点 ![]() 为极点,以
为极点,以 ![]() 轴正半轴为极轴,圆
轴正半轴为极轴,圆 ![]() 的极坐标方程为
的极坐标方程为 ![]() .
.
(1)将圆 ![]() 的极坐标方程化为直角坐标方程;
的极坐标方程化为直角坐标方程;
(2)过点 ![]()
![]() 作斜率为1直线
作斜率为1直线 ![]() 与圆
与圆 ![]() 交于
交于 ![]() 两点,试求
两点,试求 ![]() 的值.
的值.
【答案】
(1)解:由 ![]() ,可得
,可得 ![]() ,
,
∴ ![]() ,∴
,∴ ![]() ,
,
即 ![]()
(2)解:过点 ![]() 作斜率为
作斜率为 ![]() 的直线
的直线 ![]() 的参数方程为
的参数方程为 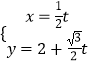 (
( ![]() 为参数).
为参数).
代入 ![]() 得
得 ![]() ,
,
设点 ![]() 对应的参数分别为
对应的参数分别为 ![]() ,则
,则 ![]() ,
, ![]() .
.
由 ![]() 的几何意义可得
的几何意义可得 ![]() .
.
【解析】(1)根据题意把直线的参数方程化为一般式即可得出化简的圆的极坐标方程运用极坐标与一般方程的互化关系即可求出圆的普通方程。(2)首先求出直线l的参数方程代入到圆的非常重得到关于t的方程结合韦达定理以及参数t的几何意义即可求出结果。

练习册系列答案
相关题目