题目内容
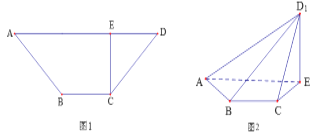
【题目】如图1所示,在等腰梯形ABCD中,![]() ,
,![]() ,垂足为E,
,垂足为E,![]() ,
,![]() 将
将![]() 沿EC折起到
沿EC折起到![]() 的位置,如图2所示,使平面
的位置,如图2所示,使平面![]() 平面ABCE.
平面ABCE.
(1)连结BE,证明:![]() 平面
平面![]() ;
;
(2)在棱![]() 上是否存在点G,使得
上是否存在点G,使得![]() 平面
平面![]() ,若存在,直接指出点G的位置
,若存在,直接指出点G的位置![]() 不必说明理由
不必说明理由![]() ,并求出此时三棱锥
,并求出此时三棱锥![]() 的体积;若不存在,请说明理由.
的体积;若不存在,请说明理由.
【答案】(1)证明见解析;(2)存在,点G为![]() 的中点,
的中点,![]() .
.
【解析】
(1)通过面面垂线的性质定理,证得![]() 平面ABCE,由此证得
平面ABCE,由此证得![]() .利用勾股定理计算证明
.利用勾股定理计算证明![]() ,从而证得
,从而证得![]() 平面
平面![]() .
.
(2)通过线面平行的判定定理,判断出点G为![]() 的中点.利用换顶点的方法,通过
的中点.利用换顶点的方法,通过![]() ,来计算出三棱锥
,来计算出三棱锥![]() 的体积.
的体积.
![]() 1
1![]() 因为平面
因为平面![]() 平面ABCE,平面
平面ABCE,平面![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面ABCE,
平面ABCE,
又因为![]() 平面ABCE,所以
平面ABCE,所以![]() ,又
,又![]() ,满足
,满足![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() .
.
![]() 2
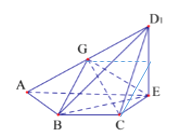
2![]() 在棱
在棱![]() 上存在点G,使得
上存在点G,使得![]() 平面
平面![]() ,
,
此时点G为![]() 的中点.
的中点.![]() ,
,
由![]() 1
1![]() 知,
知,![]() 平面ABCE,所以
平面ABCE,所以![]() ,
,
又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以CE为三棱锥![]() 的高,且
的高,且![]() ,
,
在![]() 中,
中,![]() ,G为斜边
,G为斜边![]() 的中点,
的中点,
所以![]() ,
,
所以![]() .
.
故,在棱![]() 上存在点G,使得
上存在点G,使得![]() 平面
平面![]() ,
,
此时三棱锥![]() 的体积为
的体积为![]() .
.

练习册系列答案
相关题目