题目内容
【题目】对于三次函数![]() ,给出定义:设
,给出定义:设![]() 是函数
是函数![]() 的导数,
的导数,![]() 是
是![]() 的导数,若方程
的导数,若方程![]() 有实数解
有实数解![]() ,则称点
,则称点![]() 为函数
为函数![]() 的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数
的“拐点”.经过探究发现:任何一个三次函数都有“拐点”;任何一个三次函数都有对称中心,且“拐点”就是对称中心.设函数![]() .
.
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)若不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】
(1)将![]() 代入,结合定义可求得对称中心,进而可知
代入,结合定义可求得对称中心,进而可知![]() .结合所求式子特征即可求解.
.结合所求式子特征即可求解.
(2)将![]() 代入不等式,结合定义域可分离参数
代入不等式,结合定义域可分离参数![]() ,构造函数
,构造函数![]() ,求得
,求得![]() 并令
并令![]() ,求得极值点,即可由导函数符号判断函数的单调性,进而求得
,求得极值点,即可由导函数符号判断函数的单调性,进而求得![]() ,即可确定
,即可确定![]() 的取值范围.
的取值范围.
(1)函数![]() ,
,
当![]() 时,
时,![]()
因为![]() ,
,
∴![]() ,
,
令![]() ,解得
,解得![]() ,
,
则对称中心的纵坐标为![]() ,故对称中心为
,故对称中心为![]() ,
,
所以![]() ,
,
所以![]() ,
,![]() ,…
,…
则![]() .
.
(2)∵![]() ,
,![]() ,
,
即![]() ,
,
又![]() ,
,
∴![]() 在
在![]() 上恒成立.
上恒成立.
令![]() .
.
∴![]() .
.
∵![]() ,
,
令![]() ,得
,得![]() 或
或![]() (舍去).
(舍去).
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递减;
上单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增.
上单调递增.
∴![]() .
.
∴![]() ,
,
即![]() 的取值范围为
的取值范围为![]() .
.

【题目】鱼卷是泉州十大名小吃之一,不但本地人喜欢,而且深受外来游客的赞赏.小张从事鱼卷生产和批发多年,有着不少来自零售商和酒店的客户当地的习俗是农历正月不生产鱼卷,客户正月所需要的鱼卷都会在上一年农历十二月底进行一次性采购小张把去年年底采购鱼卷的数量x(单位:箱)在![]() 的客户称为“熟客”,并把他们去年采购的数量制成下表:
的客户称为“熟客”,并把他们去年采购的数量制成下表:
采购数x |
|
|
|
|
|
客户数 | 10 | 10 | 5 | 20 | 5 |
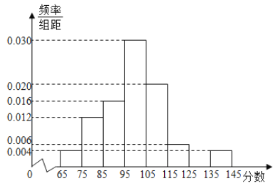
(1)根据表中的数据作出频率分布直方图,并估计采购数在168箱以上(含168箱)的“熟客”人数;
(2)若去年年底“熟客”们采购的鱼卷数量占小张去年年底总的销售量的![]() ,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
,估算小张去年年底总的销售量(同一组中的数据用该组区间的中点值为代表);
(3)由于鱼卷受到游客们的青睐,小张做了一份市场调查,决定今年年底是否在网上出售鱼卷,若不在网上出售鱼卷,则按去年的价格出售,每箱利润为20元,预计销售量与去年持平;若在网上出售鱼卷,则需把每箱售价下调2至5元,且每下调m元(![]() )销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.
)销售量可增加1000m箱,求小张今年年底收入Y(单位:元)的最大值.