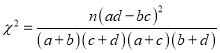题目内容
【题目】已知函数![]() .
.
(1)若![]() ,求函数
,求函数![]() 的极值;
的极值;
(2)若函数![]() 有两个零点,求实数a的取值范围.
有两个零点,求实数a的取值范围.
【答案】(1)![]() 时,
时, ![]() 取极大值
取极大值![]() ,当
,当![]() 时,
时, ![]() 取极小值
取极小值![]() .(2)
.(2)![]()
【解析】试题分析:(1)求出![]() 的导数,判断单调区间,可得极值;
的导数,判断单调区间,可得极值;
(2)根据题意可得![]() ,分
,分![]() ,
, ![]() 和
和![]() 三种情况,讨论函数的增减情况,判断函数的零点个数.
三种情况,讨论函数的增减情况,判断函数的零点个数.
试题解析:
(1)函数定义域为![]() ,
,
![]() .
.
![]() 解得
解得![]() ---1分
---1分
列表:
|
|
|
|
|
|
| + | 0 | _ | 0 | + |
|
| 极大值 |
| 极小值 |
|
所以![]() 时,
时, ![]() 取极大值
取极大值![]() ,当
,当![]() 时,
时, ![]() 取极小值
取极小值![]() .
.
(2)![]()
当![]() 时,易知函数f(x)只有一个零点,不符合题意; 当
时,易知函数f(x)只有一个零点,不符合题意; 当![]() 时,在
时,在![]() 上,
上, ![]() 单调递减;
单调递减;
在![]() 上,
上, ![]() 单调递增;
单调递增;
![]() ,且
,且![]()
所以函数![]() 有两个零点.
有两个零点.
当![]() 时,在
时,在![]() 和
和![]() 上
上![]() 单调递增;在
单调递增;在![]() 和
和![]() 上
上![]() 单调递减;
单调递减;
![]() ,函数
,函数![]() 至多有一个零点,不符合题意.
至多有一个零点,不符合题意.
当![]() 时,在
时,在![]() 和
和![]() 上
上![]() 单调递增;在
单调递增;在![]() 上
上![]() 单调递减;
单调递减;
![]() ,函数
,函数![]() 至多有一个零点,不符合题意.
至多有一个零点,不符合题意.
综上:实数a的取值范围是![]() .
.
点睛:导数是研究函数的单调性、极值(最值)最有效的工具对导数的应用的考查主要从以下几个角度进行:(1)考查导数的几何意义,往往与解析几何、微积分相联系;(2)利用导数求函数的单调区间,判断单调性;已知单调性求参数;(3)利用导数求函数的最值(极值),解决生活中的优化问题;(4)考查数形结合思想的应用.

练习册系列答案
相关题目
【题目】某校随机调查了80位学生,以研究学生中爱好羽毛球运动与性别的关系,得到下面的数据表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(1)将此样本的频率估计为总体的概率,随机调查了本校的3名学生.设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和期望值;
的分布列和期望值;
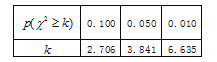
(2)根据表中数据,能否有充分证据判定爱好羽毛球运动与性别有关联?若有,有多大把握?
附: