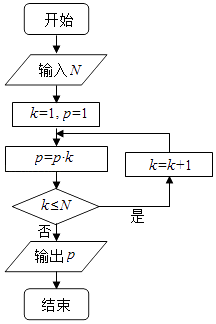
题目内容
【题目】某校随机调查了80位学生,以研究学生中爱好羽毛球运动与性别的关系,得到下面的数据表:
爱好 | 不爱好 | 合计 | |
男 | 20 | 30 | 50 |
女 | 10 | 20 | 30 |
合计 | 30 | 50 | 80 |
(1)将此样本的频率估计为总体的概率,随机调查了本校的3名学生.设这3人中爱好羽毛球运动的人数为![]() ,求
,求![]() 的分布列和期望值;
的分布列和期望值;
(2)根据表中数据,能否有充分证据判定爱好羽毛球运动与性别有关联?若有,有多大把握?
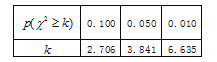
附: 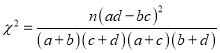
【答案】(1) ![]() (2) 没有充分证据判定爱好羽毛球运动与性别有关联.
(2) 没有充分证据判定爱好羽毛球运动与性别有关联.
【解析】试题分析:(1)![]() 的所有可能取值为
的所有可能取值为![]() ,随机变量
,随机变量![]() 服从二项分布,运用独立重复试验公式求出概率后列出分布列,运用二项分布公式求
服从二项分布,运用独立重复试验公式求出概率后列出分布列,运用二项分布公式求![]() 的期望;(2)根据列联表,利用公式
的期望;(2)根据列联表,利用公式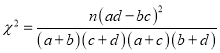 计算临界值,同临界值表进行比较,即可得到结论.
计算临界值,同临界值表进行比较,即可得到结论.
试题解析:(1)任一学生爱好羽毛球的概率为![]() ,故
,故![]() ~
~![]()
![]()
![]()
![]()
![]()
|
|
| 2 | 3 |
|
|
|
|
|
![]() 的分布列为
的分布列为

![]()
(2)![]()
故没有充分证据判定爱好羽毛球运动与性别有关联.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目