题目内容
若等比数列{an}中,前n项和Sn=3n+a,则a等于( )
| A.-4 | B.-2 | C.0 | D.-1 |
由Sn=3n+a,得:a1=3+a,
当n≥2时,an=Sn-Sn-1=(3n+a)-(3n-1+a)=2×3n-1.
因为数列{an}是等比数列,所以,an=2×3n-1对n=1时仍然成立,
则a1=3+a=2×31-1=2,
所以,a=-1.
故选D.
当n≥2时,an=Sn-Sn-1=(3n+a)-(3n-1+a)=2×3n-1.
因为数列{an}是等比数列,所以,an=2×3n-1对n=1时仍然成立,
则a1=3+a=2×31-1=2,
所以,a=-1.
故选D.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
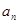 }是等差数列,数列{
}是等差数列,数列{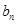 }的前
}的前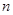 项和
项和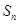 满足
满足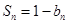 ,
,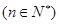 ,且
,且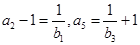
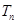 为数列{
为数列{ 已知它的前n项和Sn=6,则项数n等于 .
已知它的前n项和Sn=6,则项数n等于 .