题目内容
(文)等差数列{an}的前n项和为Sn,S30=12S10,S10+S30=130,则S20=( )
| A.40 | B.50 | C.60 | D.70 |
由等差数列的性质可得:S10,S20-S10,S30-S20成等差数列.
∴2(S20-S10)=S10+S30-S20.
∵S30=12S10,S10+S30=130,
解得S10=10,S30=120.
∴2(S20-10)=10+120-S20,
解得S20=50.
故选:B.
∴2(S20-S10)=S10+S30-S20.
∵S30=12S10,S10+S30=130,
解得S10=10,S30=120.
∴2(S20-10)=10+120-S20,
解得S20=50.
故选:B.

练习册系列答案
相关题目
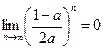 ,则a的取值范围是( )
,则a的取值范围是( )
 或
或

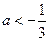 或
或