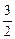题目内容
(本小题满分14分)设数列{an}和{bn}满足a1=b1=6,a2=b2=4,a3=b3=3,且数列{an+1-an}是等差数列,数列{bn―2}是等比数列(n∈N*).
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)是否存在k∈N*,使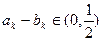 ?若存在,求出k,若不存在,说明理由.
?若存在,求出k,若不存在,说明理由.
(Ⅰ)求数列{an},{bn}的通项公式;
(Ⅱ)是否存在k∈N*,使
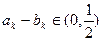 ?若存在,求出k,若不存在,说明理由.
?若存在,求出k,若不存在,说明理由.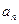 =
=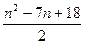 ,
,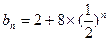
不存在k∈N*,使存在k∈N*,使
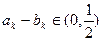
解:(Ⅰ)由条件知a2-a1=―2,a3―a2=―1;
∵{an+1-an}是等差数列,
∴首项a2―a1=―2,公差d=(a3―a2)―(a2―a1)=1;
∴an+1―an=―2+(n―1)d=n―3. …………………2分
当n≥2时,
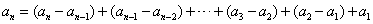
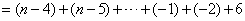
=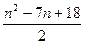 ;
;
当n=1时也满足,∴n∈N*,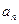 =
=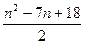 . …………………5分
. …………………5分
∵{bn―2}是等比数列,首项b1―2=4,b2―2=2,∴公比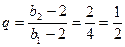 ;
;
∴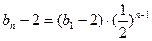 ,
,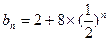 . …………………8分
. …………………8分
(Ⅱ)设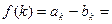
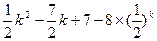 =
=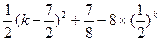 ,
,
当k≥4时,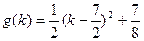 为
为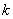 的单增函数,
的单增函数,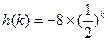 也为
也为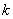 的单增函数,
的单增函数,
∴k≥4时,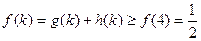 .…………………12分
.…………………12分
∵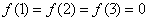 ,∴不存在k∈N*,使存在k∈N*,使
,∴不存在k∈N*,使存在k∈N*,使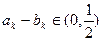 .
.
…………………14分
∵{an+1-an}是等差数列,
∴首项a2―a1=―2,公差d=(a3―a2)―(a2―a1)=1;
∴an+1―an=―2+(n―1)d=n―3. …………………2分
当n≥2时,
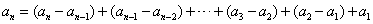
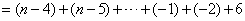
=
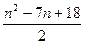 ;
;当n=1时也满足,∴n∈N*,
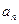 =
=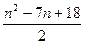 . …………………5分
. …………………5分∵{bn―2}是等比数列,首项b1―2=4,b2―2=2,∴公比
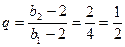 ;
;∴
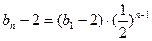 ,
,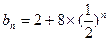 . …………………8分
. …………………8分(Ⅱ)设
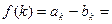
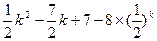 =
=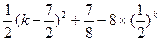 ,
,当k≥4时,
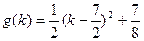 为
为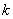 的单增函数,
的单增函数,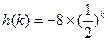 也为
也为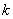 的单增函数,
的单增函数,∴k≥4时,
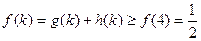 .…………………12分
.…………………12分∵
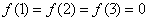 ,∴不存在k∈N*,使存在k∈N*,使
,∴不存在k∈N*,使存在k∈N*,使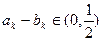 .
.…………………14分

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
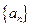 满足
满足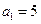 ,
, 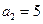 ,
,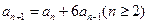 .
.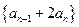 是等比数列
是等比数列 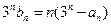 ,且
,且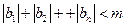 对于
对于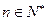 恒成立,求
恒成立,求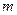 的取值范围
的取值范围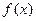 是定义在R上的不恒为零的函数,且对于任意的
是定义在R上的不恒为零的函数,且对于任意的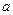 、
、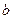 ∈R,都满足
∈R,都满足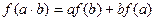 ,若
,若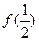 =1,
=1,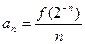 ;
;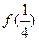 、
、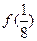 、
、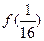 的值;
的值;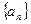 的通项公式,并用数学归纳法证明。
的通项公式,并用数学归纳法证明。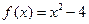 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ?N *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ?N *),x1=4.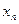 表示xn+1;
表示xn+1;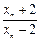 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;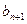 与
与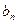 的大小.
的大小.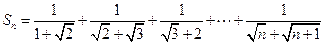 ,若
,若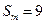 ,则
,则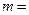 __▲
__▲ 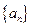 满足
满足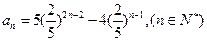 ,若
,若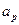 和
和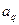 分别为数列中的最大项和最小项,则
分别为数列中的最大项和最小项,则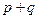 =(★)
=(★)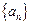 满足
满足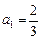 ,且对任意的正整数
,且对任意的正整数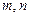 ,都有
,都有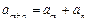 ,则
,则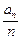 等于( )
等于( )