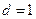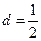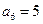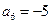题目内容
已知函数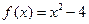 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ?N *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ?N *),x1=4.
(Ⅰ)用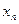 表示xn+1;
表示xn+1;
(Ⅱ)记an=lg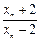 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;
(Ⅲ)若bn=xn-2,试比较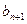 与
与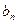 的大小.
的大小.
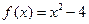 ,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ?N *),x1=4.
,设曲线y=f(x)在点(xn,f(xn))处的切线与x轴的交点为(xn+1,0)(n ?N *),x1=4.(Ⅰ)用
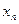 表示xn+1;
表示xn+1;(Ⅱ)记an=lg
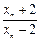 ,证明数列{an}成等比数列,并求数列{xn}的通项公式;
,证明数列{an}成等比数列,并求数列{xn}的通项公式;(Ⅲ)若bn=xn-2,试比较
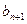 与
与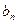 的大小.
的大小.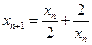 ,
,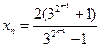 ,
,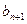 <
<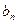
解:(Ⅰ)由题可得
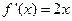 ................2分
................2分所以曲线
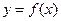 在点
在点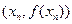 处的切线方程是:
处的切线方程是: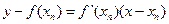 .
.即
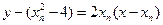 . ...............4分
. ...............4分令
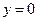 ,得
,得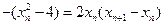 ,即
,即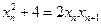 .
.显然
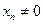 ,∴
,∴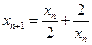 . ..................6分
. ..................6分(Ⅱ)由
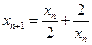 ,知
,知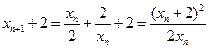 ,同理
,同理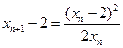 .
.故
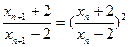 .
.从而
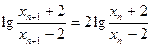 ,即
,即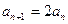 .所以,数列
.所以,数列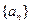 成等比数列. ...8分
成等比数列. ...8分故
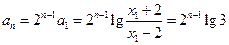 ,即
,即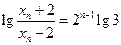 ,从而
,从而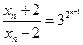 ,
,所以
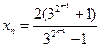 . ..................10分
. ..................10分(Ⅲ)由(Ⅱ)知
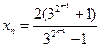 ,
,∴
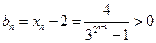 ; ...........12分
; ...........12分∴
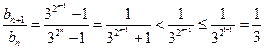 ,
, 故
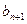 <
<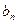 . ............14分
. ............14分
练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
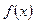 与数列
与数列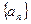 满足关系:(1) a1.>a, 其中a是方程
满足关系:(1) a1.>a, 其中a是方程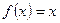 的实根,(2) an+1=
的实根,(2) an+1=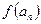 (n
(n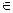 N+ ) ,如果
N+ ) ,如果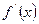 <1
<1 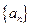 中,
中,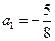 ,
,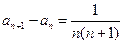 (
(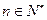 )
)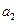 、
、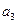 的值;
的值;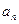 ;
;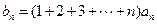 ,求
,求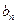 的最小值.
的最小值.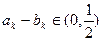 ?若存在,求出k,若不存在,说明理由.
?若存在,求出k,若不存在,说明理由.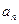 = .
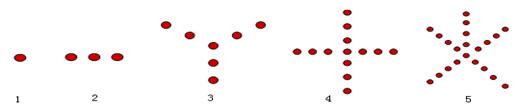
= .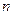 个图形中的点数
个图形中的点数 .
.
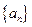 是等差数列,
是等差数列,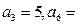 11且,
11且,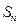 是数列
是数列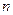 项和。
项和。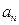 及前
及前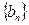 满足
满足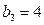 ,
,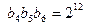 ,数列
,数列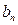
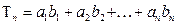 ,求
,求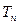 的值。
的值。 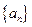 共有10项,并且其偶数项之和为30,奇数项之和为25,由此得到的结论正确的是( )
共有10项,并且其偶数项之和为30,奇数项之和为25,由此得到的结论正确的是( )