题目内容
哈六中体育节进行定点投篮游戏，已知参加游戏的甲、乙两人，他们每一次投篮投中的概率均为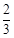
，且各次投篮的结果互不影响．甲同学决定投5次，乙同学决定投中1次就停止，否则就继续投下去，但投篮次数不超过5次．（12分）
（1）求甲同学至少有4次投中的概率；
（2）求乙同学投篮次数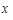
的分布列和数学期望．
（1）
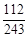；（2）分布列见解析，数学期望为
.
解析试题分析：（1）由题可知概率符合n次独立重复实验发生m次的概率，其中甲同学至少有4次投中，包括投中四次与投中五次，满足二项分布，可得
，求
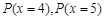即可；(2) 求乙同学投篮次数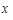的可能取值为
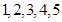，分别求出对应的概率，写出分布列，求出数学期望.
试题解析：（1）设甲同学在5次投篮中，有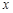
次投中，“至少有4次投中”的概率为
，则
=
=
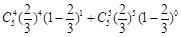． 4分
（2）由题意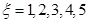
．
，
，
，
，
．
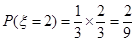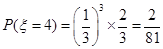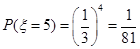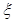的分布表为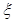1 2 3 4 5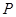 
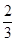
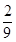
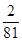
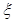的数学期望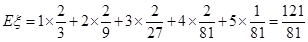
． 12分
考点：二项分布，离散型随机变量的分布列，离散型随机变量的期望.
练习册系列答案
津桥教育计算小状元系列答案
相关题目
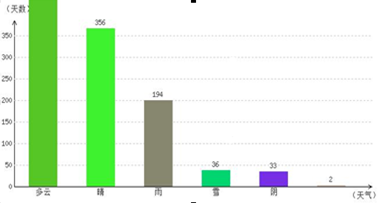
的概率乘公交或打出租的方式上班（每天一次，且交通方式仅选一种），每天交通费用相应为2元或40元；在非雨雪天的情况下，他以90%的概率骑自行车上班，每天交通费用0元；另外以10%的概率打出租上班，每天交通费用20元。（以频率代替概率，保留两位小数．参考数据：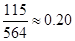
）
（单位：元），求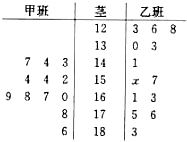
、
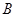两盒中都有红球、白球，且球的形状、大小都相同，盒子
个红球与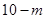
个白球，盒子
）．
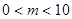表示红球的个数；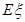
等于定值；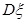
取到最小值，并求出最小值．
：在第一次取到红球后，以后两次都取到白球，事件
：在第一次取到白球后，以后两次都取到红球，若概率
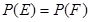，求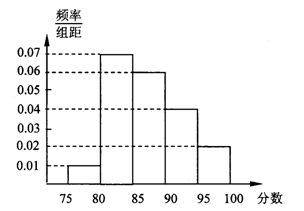
、
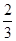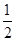，他们考核所得的等级相互独立．